Проектирование системы профилактики АТС. Оценка количественных характеристик надёжности на примере автобуса МАЗ-103, страница 8

МАЗ-103 ЕЕ 288

151335

–

МАЗ-103 ЕЕ 078

167324

174293

МАЗ-103 ЕЕ 251

130670

173070

МАЗ-103 ЕЕ 091

150582

–

МАЗ-103 ЕЕ 070

165098

–

МАЗ-103 ЕЕ 268

145673

–

МАЗ-103 ЕЕ 077

144422

–

МАЗ-103 ЕЕ 072

162965

–

МАЗ-103 ЕЕ 075

140345

–

МАЗ-103 ЕЕ 253

144403

–

МАЗ-103 ЕЕ 082

107775

–

МАЗ-103 ЕЕ 252

159865

–

МАЗ-103 ЕЕ 283

167350

–

МАЗ-103 ЕЕ 289

155377

–

4 Оценка затрат на поддержание автобуса МАЗ-103 ЕЕ 075 в исправном и работоспособном состоянии

Оценка затрат проводилась на примере автобуса МАЗ-103 с государственным номером ЕЕ 075 в эксплуатационный период с 17.02.2009 по 12.09.2011 г. Результаты оценки представлены в виде гистограммы на рисунке 4.1.

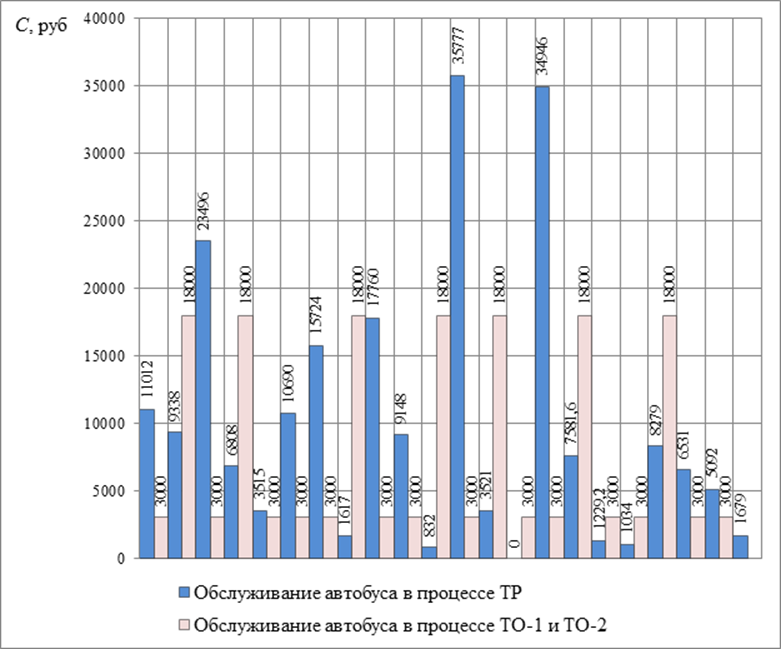
Рисунок 4.1 – Оценка затрат на поддержание работоспособного состояния автобуса МАЗ-103 ЕЕ 075

Суммарные затраты на поддержание исправного и работоспособного состояния автобуса за рассматриваемый эксплуатационный период составляет 383609,8 рублей, из которых затраты на ТО составили 168000 рублей; затраты на ТР – 215609,8 рублей.

Средняя величина годовых затрат составила 208981,46 руб.

Средняя величина ежедневных затрат составила 572,55 руб.

5 Оценка показателей свойств надёжности

Вариационный ряд:

49 57 58 65 65 74 78 78 84 90 101 106 114 126 131 134 138 146 152 158 162 164 173 184 187 201 226 227 234 238 243 248

Количество членов вариационного ряда N = 32.

Выборочная средняя определяется по формуле

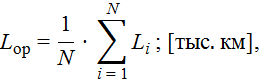
где L_i – i-ый член рассматриваемого вариационного ряда.

Выборочная средняя

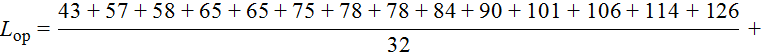
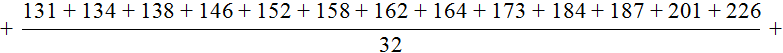
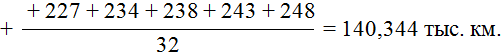
Несмещённая дисперсия определяется по формуле

Несмещённая дисперсия

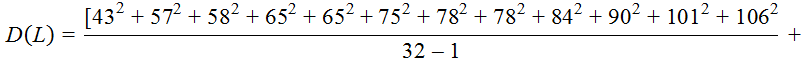
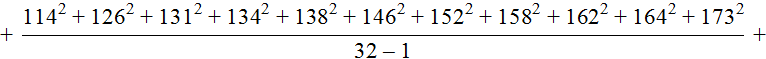
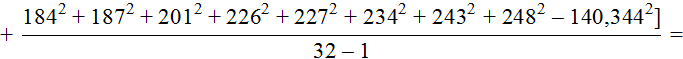
Среднее квадратическое отклонение определяется по формуле

Среднее квадратичное отклонение

Коэффициент вариации определяется по формуле

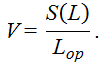
Коэффициент вариации

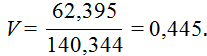
Для данной работы принимаем уровень значимости ε = 0,05.

Параметр формы b для закона Вейбулла-Гнеденко определяется в зависимости от коэффициента вариации. Исходя из данных справочной таблицы [31] для имеющегося коэффициента вариации параметр формы b = 2,4234.

Значение квантилей распределения принимается на основе удвоенного количества членов вариационного ряда и принятого уровня значимости. По данным справочной таблицы [31] принимаем   = 46,595.

Предельная относительная ошибка оценки показателя надёжности определяется по формуле

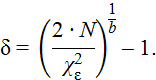
Предельная относительная ошибка оценки показателя надёжности

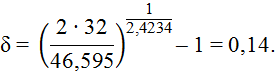
Границы доверительных интервалов определяются по формуле

L_{ср. н/в.} = L_ср ∙ (1 ± δ); [тыс. км].

Нижняя граница доверительного интервала

L_{ср. н.} = L_ср ∙ (1 – δ) = 140,344 ∙ (1 – 0,14) = 120, 696 тыс. км.

Верхняя граница доверительного интервала

L_{ср. в.} = L_ср ∙ (1 + δ) = 140,344 ∙ (1 + 0,14) = 159, 992 тыс. км.

Значение гамма-функции при V = 0,445 по данным справочной таблицы [31] составляет Г = 0,8866.

Точечная оценка параметра масштаба Вейбулла-Гнеденко определяется по формуле

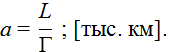
Средняя интервальная оценка параметра масштаба

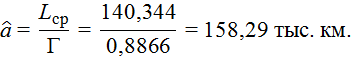
Нижняя граница интервальной оценки

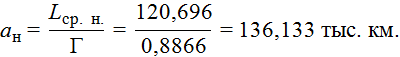
Верхняя граница интервальной оценки

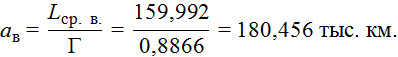
6 Проверка нулевой гипотезы

Количество интервалов рассчитывается по правилу Штюргеса:

S = 1 + 3,32 ∙ lgN.

Количество интервалов наработки

S = 1 + 3,32 ∙ lg32 = 6.

Число степеней свободы определяется по формуле

k = S – 1 – r, где r – количество параметров предполагаемого распределения.

Для данной работы принимаем r = 3.

Число степеней свободы

k = 6 – 1 – 3 = 2.

Критическая точка критерия согласия Пирсона определяется исходя из справочной таблицы [31] в зависимости от числа степеней свободы и принятого уровня значимости. Для данного случая имеем  = 5,992.

Наибольший член вариационного ряда наработок L_max = 248 тыс. км.

Наименьший член вариационного ряда наработок L_min = 49 тыс. км.

Протяжённость интервала определяется по формуле

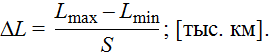
Протяжённость интервала