Проектирование системы профилактики АТС (на примере автобусов МАЗ-103), страница 6

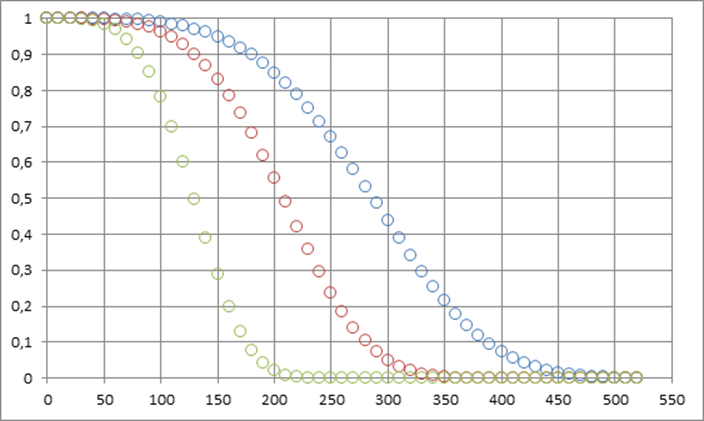
Рисунок 1 – График вероятности безотказной работы пневмобаллона до первого отказа

2.Оценка гамма – процентной наработки до отказа

По данному графику можно оценить гамма – процентную наработку до первого отказа. Для этого параллельно оси абсцисс проводят прямую линию через точку P(L) = j=100%. Пусть j = 90%. Тогда P(L) = 0,9. Абсциссы точек пересечения этой прямой с кривыми P(L) – дают точечную и интервальную оценки гамма – процентной наработки до первого отказа. Для более точной оценки используем формулу и получаем следующие оценки:

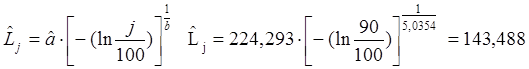
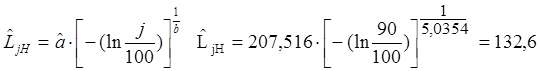
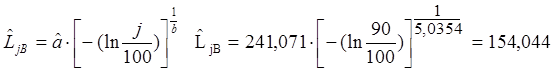
3.Оценка интенсивности отказов

Интенсивность отказов  – условная плотность вероятности возникновения отказа невосстанавливаемого элемента АТС, определяемая для рассматриваемого момента времени при условии, что до этого времени отказ не возник.

Для закона Вейбулла-Гнеденко его точечная оценка, тыс. км:

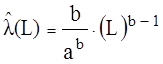
Таблица 5 – Точечная оценка интенсивности отказов пневмобаллона