Проектирование системы профилактики АТС (на примере автобусов МАЗ-103), страница 5

Так как в таблице нет нужного нам значения коэффициента , то разбиваем имеющийся у нас коэффициент на сумму коэффициентов:

V = 0.220 + 0.008

β = β’ + β^x

β’ = 5.2254

Имеем: V = 0.22 => β’ = 5.2254

V = 0.24 => β” = 4.7505

∆β = 5.2254 – 4.7505 = 0.4749

Имеем пропорцию: 0.02/0.4749 = 0.008/x, х = 0.1899

Отсюда β = 5.2254 – 0.1899 = 5.0354

Определим δ при α = 0.90, для чего рассчитаем уровень значимости ε и выберем из таблицы значение

Е = 0.05

 = 34.764

δ =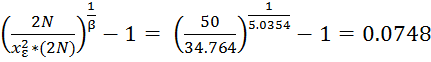

3.Интервальная оценка

Границы доверительного интервала, тыс.км.,

L_{ср н} = L_ср*(1- δ) = 206.92 * (1-0.0748) = 191.4424

L_{ср в}  = L_ср*(1+ δ) = 206.92 * (1+0.0748) = 222.3976

В ходе расчётов получены точечная и интервальные оценки средней наработки до первого отказа:

L_cp  = 206.92; L_{ср н} = 191.4424; L_{ср в}  = 222.3976.

Это означает, что действительное значение наработки до отказа находиться в интервале [191.4424 тыс.км.; 222.3976тыс.км.] с вероятностью 0.90.

Значение гамма-функции:

Г  (1+1/δ)

Так как в таблице нет нужного нам значения коэффициента Г, разбиваем имеющийся у нас коэффициент на сумму коэффициентов:

0,228 = 0.22 + 0.008

х = х’ + х^x

Имеем: Г = 0.22 => х’ = 0.9205

Г = 0.24 => х’ = 0.9154

0.02 = 0.0051

0.008 = х

Имеем пропорцию: 0.008*0.0051/0.02 = 0.00204

Отсюда Г = 0.9205 - 0.00204 = 0.91846

Точечная оценка параметра масштаба закона Вейбулла – Гнеденко, тыс.км.:

а = 206.92/0.91846 =225,290

а_н = 191.4424/0.91846   = 208,438

а_в = 222.3976/0.91846  = 242,141

Проверка нулевой гипотезы

Рассчитать количество интервалов S по правилу Штюргерса с округлением до целого значения:

S = 1 + 3.32 lg N

S = 1 + 3.32*1.3979 = 5.6410

Разделить на S интервалов размах вариационного ряда, т.е. разность между наибольшим и наименьшим числами. Границы интервалов определим по формуле:

∆L_i =

∆L_i = 23.166

Определим расчётное значение критерия:

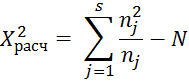
Проверим выполнимость нулевой гипотезы:

= 36.1 - 25 = 11.1

Видим, что условие χ²_рас < χ²_табл выполняется, следовательно, выполняется и нулевая гипотеза.

Таблица 3 – Расчёт Х² - критерия согласия Пирсона

I	Li-1	Li+1	ni	ni2	∆F(Li)	i	n2i/i
1	0	162.16	5	25	0.178	4.45	5.6
2	162.16	185.326	5	25	0.139	3.475	7.19
3	185.326	208.492	4	16	0.181	4.525	3.535
4	208.492	231.658	2	4	0.191	4.775	0.83
5	231.658	254.824	3	9	0.162	4.05	2.22
6	254.824	277.99	6	36	0.089	2.225	16.1
7	277.99	∞	1	1	0.061	1.525	0.655
Итого:                                            25           115          1.000        25.000         36.1

Оценка количественных характеристик безотказности и долговечности

1.Оценка вероятности безотказной работы

Согласно ГОСТ 27.002-83 вероятность безотказной работы P(L) есть вероятность того, что в пределах заданной наработки отказ элемента АТС не возникнет.

Вероятность безотказной работы оценивается по закону Вейбулла-Гнеденко:

Р = EXP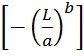

Таблица 4 – Точечная оценка вероятности безотказной работы пневмобаллона до первого отказа