Границы доверительного интервала, тыс.км:
Lсрн = 103,5*(1-0,1)= 93,15
Lсрв = 103,5*(1+0,1)= 113,85
Lср = 103,5
Значение гамма-функции определим из таблицы 4 [31] в зависимости от полученного значения коэффициента вариации:
![]() = 0,8961
= 0,8961
Точечная оценка параметра масштаба закона Вейбулла-Гнеденко, тыс.км:
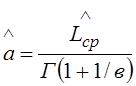
![]()
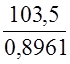 =115,5
=115,5
Граничные значения интервальной оценки, тыс.км:
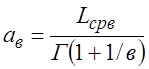
![]() = 93,15/0,8961=103,95
= 93,15/0,8961=103,95
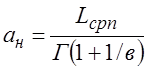
![]() =113,85/0,8961=127,05
=113,85/0,8961=127,05
3. Проверка нулевой гипотезы
χ2рас < χ2табл(β,k) – условие соблюдение нулевой гипотезы, где χ2рас – значение критерия согласия Пирсона, вычисленное по эксперимен- тальным данным; χ2табл – критическая точка критерия ( по таблице № 2 [31] );
где β – уровень значимости, k – число степеней свободы,
β = 0,1; где S – количество частных интервалов выборки,
r – количество параметров предлагаемого распределения,
r = 2.
Количество интервалов S по правилу Штюргеса:
![]()
![]()
![]()
k = S – l – r
k = 6-1-2=3;
Так как k=3, то ![]() =11,345 (таблица №2 [31] )
=11,345 (таблица №2 [31] )
Протяжённость интервала(тыс.км.):
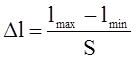
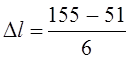
![]()
где Lmax – наибольший элемент Lmin – наименьший элемент;
- границы интервалов определяют по формуле
![]()
где j=1, 2, …, s.
![]()
![]()
![]()
![]()
![]()
Расчёт теоретических частот:
![]()
![]()
Для закона Вейбулла-Гнеденко функцию распределения отказов определяют по следующей формуле:
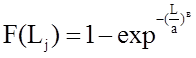
![]()
![]()
![]()
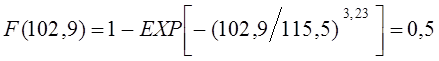
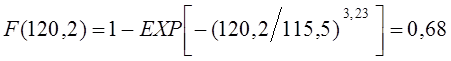
![]()
 где F(Lj) – функция распределения отказов;
где F(Lj) – функция распределения отказов;
ΔF(Li) = F(Li+1) - F(Li).
![]()
![]()
![]()
![]()
![]()
![]()
Значит ![]() равно:
равно:
![]() =34 * 0,18= 6,12
=34 * 0,18= 6,12
![]() = 34 *
0,14 = 5,1
= 34 *
0,14 = 5,1
![]() =34* 0,18
= 6,12
=34* 0,18
= 6,12
![]() = 34 *
0,18 = 6,12
= 34 *
0,18 = 6,12
![]() = 34 *
0,15 = 5,1
= 34 *
0,15 = 5,1
![]() = 34 *
0,17 =5,78
= 34 *
0,17 =5,78
Таблица 1 - Расчет ![]() - распределения согласия Пирсона
- распределения согласия Пирсона
|
j |
Lj |
Lj+1 |
nj |
nj2 |
ΔF(Lj) |
nj |
nj2 /nj |
|
1 |
0 |
68,3 |
10 |
100 |
0,17 |
5,78 |
17,3 |
|
2 |
68,3 |
85,6 |
3 |
9 |
0,14 |
5,1 |
1,76 |
|
3 |
85,6 |
102,9 |
2 |
4 |
0,18 |
6,12 |
0,65 |
|
4 |
102,9 |
120,2 |
6 |
36 |
0,18 |
6,12 |
5,88 |
|
5 |
120,2 |
137,5 |
5 |
25 |
0,15 |
5,1 |
4,9 |
|
6 |
137,5 |
|
8 |
64 |
0,17 |
5,78 |
11,07 |
|
34 |
1 |
41,58 |
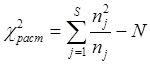
![]()
χ2расчетное = 7,58 < χ2табличное= 11,345
Вывод: гипотеза подтверждается, так как χ2табличное > χ2расчетное .
4.Оценка количественных характеристик безотказности и долговечности
1.Оценка вероятности безотказной работы
Согласно ГОСТ 27.002 – 83 вероятность безотказной работы P(L) есть вероятность того, что в пределах заданной наработки на отказ элемента АТС не возникнет. Статистически определяется по приближенной формуле:
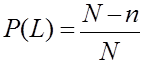 , где n – количество
отказавших элементов за пробег от 0 до L;
, где n – количество
отказавших элементов за пробег от 0 до L;
N – Общее количечество элементов, находящихся под наблюдением.
Известно, что вероятность безотказной работы и вероятность отказа составляют полную группу событий:
P (L) +F (L) =1
По закону Вейбулла-Гнеденко
![]()
По нормальному закону
P(L)=1 – Ф(z),
где ![]()
Интервальную оценку ![]() определяют, подставив соответственно
определяют, подставив соответственно ![]() и
и ![]() (или
(или ![]() и
и ![]() ).
).
Таблица 2 – Вероятность безотказной работы
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.