Расчет коэффициента корреляции для номенклатур запасной части

1.  Расчет коэффициента корреляции

Заданы продажи пяти номенклатур (k, l, т, п, h) запасной части в магазине в течение 12 месяцев.

1.  Необходимо определить коэффициенты корреляции между всеми сочетаниями номенклатур и вычисления сведите в матрицу

2.  Для тех сочетаний номенклатур, для которых , , построить диаграммы рассеивания.

Таблица 1 - Продажи пяти номенклатур запасной части в магазине в течение 12 месяцев

Рассмотрим алгоритм расчета коэффициента корреляции для сочетания номенклатур k и l.

1)  Определяем среднее значение спроса по k-й и l-й номенклатуре запасных частей:

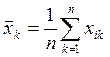
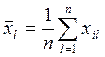                                                     (1)

2)  Находим эмпирические дисперсии:

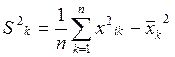
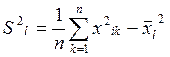                                    (2)

3)  Вычисляем эмпирическую ковариацию:

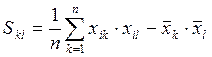                                  (3)

4)  Рассчитываем коэффициент корреляции:

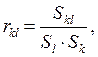
                                      (4)

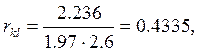
По аналогичному алгоритму произведем расчет других сочетаниями номенклатур, для удобства расчеты сведем в таблицу.

Таблица 2 – Матрица коэффициентов вариации

По итогам значений коэффициентов корреляции строим диаграммы рассеивания, для тех сочетаний номенклатур, для которых , ,

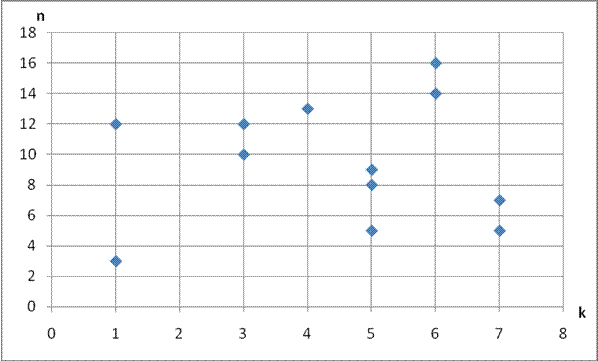
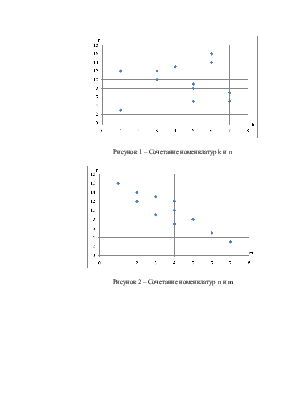
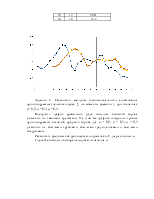
Рисунок 1 – Сочетание номенклатур k и n

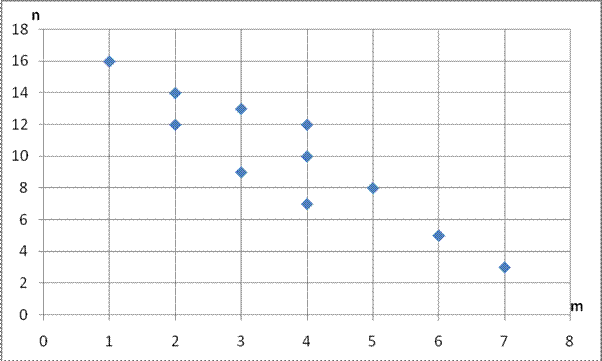
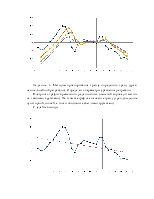
Рисунок 2 – Сочетание номенклатур n и m

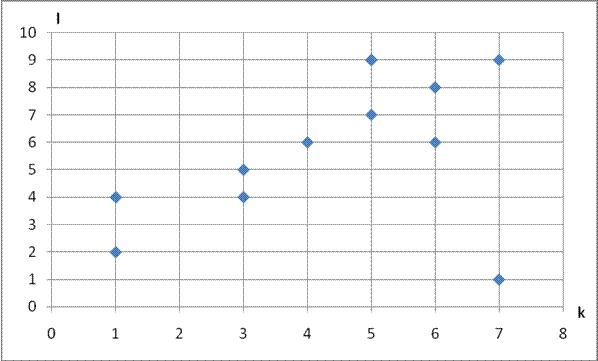
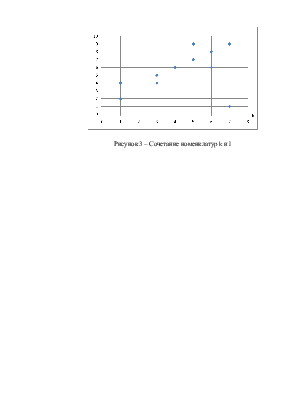
Рисунок 3 – Сочетание номенклатур k и l

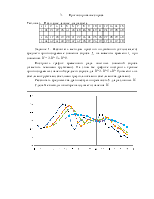
2.   Регрессионный анализ спроса

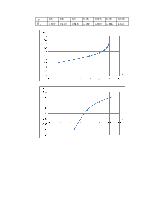
Проводится исследование спроса на запасные части. Данные о зависимости спроса от цены, по результатам пробных продаж, представлены в табл. 3. Требуется построить прямую регрессии X от Y.

Для определения параметров а и b по формуле (5) сведем данные в табл. 3.

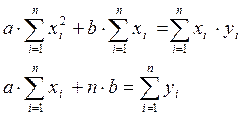                                      (5)

Теперь запишем систему (5) с учетом найденных по табл. 3 значений:

9455а + 465b = 5568, 465а + 15b = 353.

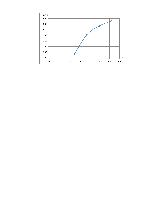
Такую систему легко решить: а = -3.72; b = 138.85. Окончательно получаем уравнение регрессии у = -3,72х + 138,85.

Определим ошибку уравнения регрессии. Промежуточные расчеты приведены в табл. 4.