Другие предметы \ Научно-исследовательская работа студента

Расчет коэффициента корреляции для номенклатур запасной части, страница 2

(y-(ax+b))^2

1

11

135,13

15408,26

2

10

131,41

14740,39

3

11

127,69

13616,56

4

11

123,97

12762,22

5

11

120,25

11935,56

6

12

116,53

10926,52

7

11

112,81

10365,28

8

12

109,09

9426,468

9

12

105,37

8717,957

10

11

101,65

8217,423

11

13

97,93

7213,105

12

13

94,21

6595,064

13

12

90,49

6160,68

14

13

86,77

5442,013

15

12

83,05

5048,103

16

9

79,33

4946,309

17

9

75,61

4436,892

18

8

71,89

4081,932

19

10

68,17

3383,749

20

12

64,45

2751,003

21

16

60,73

2000,773

22

17

57,01

1600,8

23

15

53,29

1466,124

24

13

49,57

1337,365

25

12

45,85

1145,823

26

13

42,13

848,5569

27

13

38,41

645,6681

28

11

34,69

561,2161

29

10

30,97

439,7409

30

10

27,25

297,5625

Сумма

176519,1

Ошибка уравнения регрессии δ=108,48


3.  Прогнозирование спроса

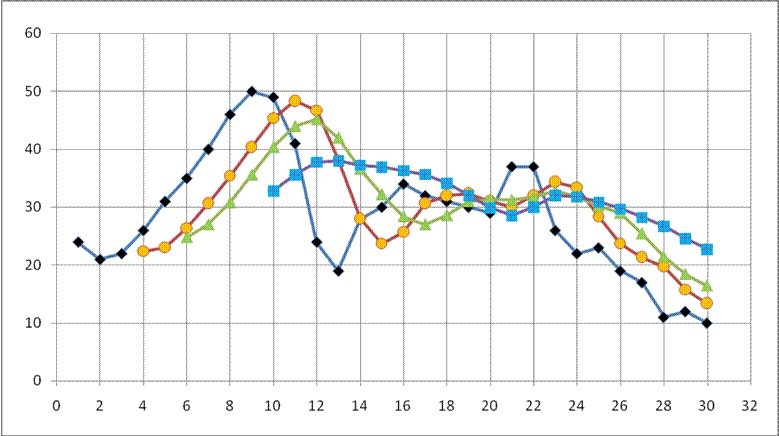
Таблица 4 – Исходные данные для расчета

t

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

x

24

21

22

26

31

35

40

46

50

49

41

24

19

28

30

t

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

x

34

32

31

30

29

37

37

26

22

23

19

17

11

12

10

Задание 1. Рассчитать методом простого подвижного (скользящего) среднего прогнозируемые значения спроса  на моменты времени  при значениях N = 3,N= 5 и N=9.

Построить график временного ряда опытных значений спроса (отметить темными кружками). На этом же графике построить кривые прогнозируемых значений среднего спроса для N=3, N=5 и N=9 (отметить их светлыми кружками, светлыми треугольниками и светлыми квадратами).

Рассчитать среднюю квадратическую погрешность δ для различных N.

Сделайте выводы о выборе наилучшего значения N.


Скачать файл