Расчет коэффициента корреляции для номенклатур запасной части, страница 5

Сделайте выводы.

t	x	t^2	tx
1	24	1	24
2	21	4	42
3	22	9	66
4	26	16	104
5	31	25	155
6	35	36	210
7	40	49	280
8	46	64	368
9	50	81	450
10	49	100	490
11	41	121	451
12	24	144	288
13	19	169	247
14	28	196	392
15	30	225	450
16	34	256	544
17	32	289	544
18	31	324	558
19	3	361	57
20	29	400	580
21	37	441	777
22	37	484	814
23	26	529	598
24	22	576	528
25	23	625	575
26	19	676	494
27	17	729	459
28	11	784	308
29	12	841	348
30	10	900	300
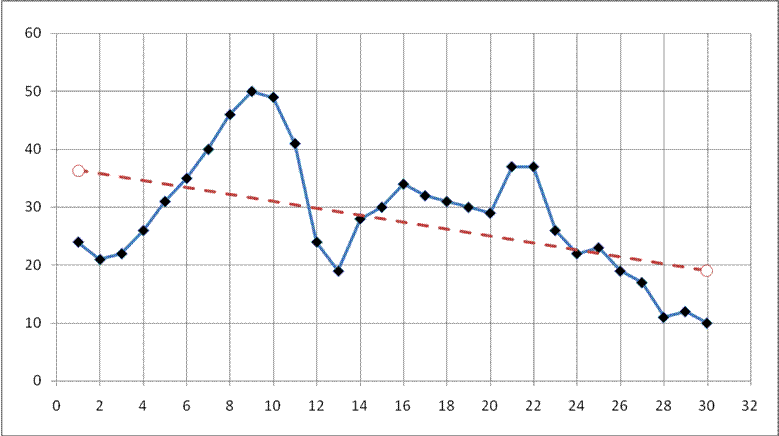
465	829	9455	11501

а=-0,6

b=36,93

Уравнение регрессии имеет вид: x=-0,6*t+36,93

4.  Прогнозирование расхода запасных частей при проектировании новой модели автомобиля

Согласно заданному варианту определите среднее число замен , число замен с учетом верхней доверительной границы .

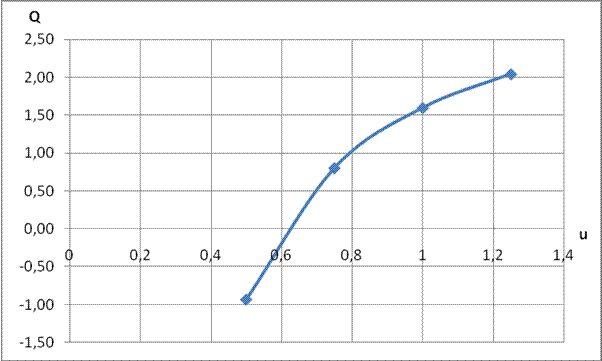
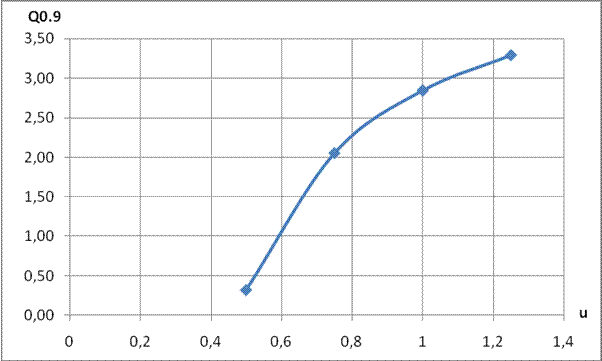
Определите  и  для трех различных параметров закона распределения скорости (интенсивности) изнашивания: (0,5, 0,5); (0,75, 0,75); (1,25, 1,25). Результаты сведите в таблицу. Постройте графики   и . На основе анализа полученных результатов сделайте выводы.

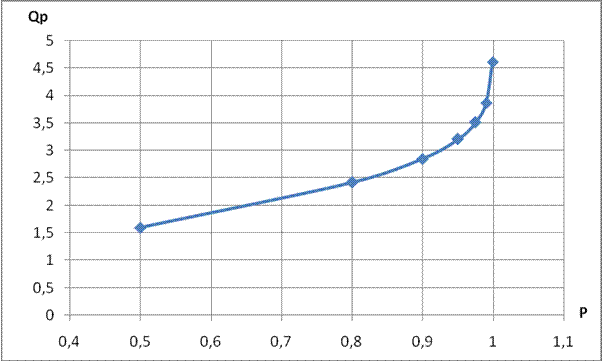
Определить  для различных Р. Построить график . На основе анализа полученных результатов сделайте выводы.

Сделайте выводы в целом по проделанной работе.

Таблица – Исходные данные

	Вариант		α
0	16	100	0,8	50	15	1	0,33	60	20	1,3	0,4
1						0,500	0,165
2						0,750	0,248
3						1,250	0,413

Вариант	0		1		2		3
		132,96		316,23		190,50		100,59
		59,30		59,30		59,30		59,30
		72,47		72,47		72,47		72,47
		42,55		42,55		42,55		42,55
		1,60		-0,93		0,80		2,04
		2,85		0,32		2,05		3,29