1 Структурный анализ технологического механизма
Механизм состоит из пяти подвижных звеньев и одного неподвижного звена (стойки), соединенных между собой шестью вращательными (О1, О2, А, В, С, D) и одной поступательной (Е) кинематическими парами.
Степень подвижности механизма определяется по формуле Чебышева
W = 3n – 2 pн – pв , (1)
где n – число подвижных звеньев механизма, n = 5;
pн – число низших кинематических пар, pн = 7 (О1, О2, А, В, С, D, Е);
pв – число высших кинематических пар, pв = 0.
![]() .
.
Механизм имеет одну степень подвижности, что соответствует одному ведущему звену. Ведущим звеном механизма является стержень О1А. Кроме того, механизм имеет в своем составе один шатун – звено 4, представляющее собой тонкий однородный стержень CD. Коромысло (звено 3) представляет собой треугольник АBC, образованный посредством неподвижного соединения стержней АB, АC и BC. Звено 5 является ведомым звеном механизма и представляет собой ползун, или, в данном случае, резцовую призму.
Образован механизм последовательным присоединением к группе Ассура I класса 1 вида (ведущему звену со стойкой) группы Ассура II класса 1 вида(звенья 2 и 3, кинематические пары А, В, О2), а затем группы Ассура II класса 3 вида (звенья 4 и 5, кинематические пары С, D, Е). Составляющие механизм группы Ассура представлены в графической части курсовой работы.
Формула строения механизма: ГА I (1) + ГА II (1) + ГА II (3).
Наивысший класс присоединенных групп – второй, поэтому механизм по классификации академика Артоболевского следует отнести к механизмам II класса.
2 Кинематический анализ механизма
2.1 Построение плана положений механизма и круговой циклограммы движения ползуна
Построение начинаем с
вычерчивания 12 положений ведущего звена. Принимаем масштаб плана положений 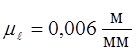 . Масштаб
. Масштаб ![]() принят
таким, чтобы план положений занял все отведенное для него место на чертеже. В
соответствии с выбранным масштабом определяем длины звеньев механизма на
чертеже, а также координаты шарниров и положение направляющей.
принят
таким, чтобы план положений занял все отведенное для него место на чертеже. В
соответствии с выбранным масштабом определяем длины звеньев механизма на
чертеже, а также координаты шарниров и положение направляющей.
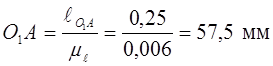
Дальнейший расчет сводим в таблицу.
Таблица 2 – Расчет длин звеньев и координат неподвижных шарниров механизма на плане положений
|
Звенья и стержни механизма |
|
|
|
|
|
|
x |
y |
|
Действитель-ная длина, м |
0,25 |
0,54 |
0,42 |
0,54 |
0,5 |
0,96 |
0,5 |
0,5 |
|
Длина на плане, мм |
41,6 |
90 |
70 |
90 |
83,3 |
160 |
83,3 |
83,3 |
Все построения на плане положений выполняем сплошными тонкими линиями. Одно произвольно выбранное положение выделяем сплошной толстой основной линией.
Для составления
круговой циклограммы движения ползуна предварительно вычерчиваем диаграмму силы
полезного сопротивления движению ползуна ![]() .
.
Крайним левым
положением ползуна на направляющей является положение D1, а положение D7 – крайним правым. Таким
образом, полный ход ползуна ![]() . Учитывая, что сила
полезного сопротивления в соответствии с заданием начинает действовать на
ползун на расстоянии 0,05Н от его крайнего левого положения и
заканчивает действие на расстоянии 0,05Н от крайнего правого положения,
определяем величину рабочего хода ползуна:
. Учитывая, что сила
полезного сопротивления в соответствии с заданием начинает действовать на
ползун на расстоянии 0,05Н от его крайнего левого положения и
заканчивает действие на расстоянии 0,05Н от крайнего правого положения,
определяем величину рабочего хода ползуна: ![]() .
Начало рабочего хода приходится на участок между положениями ползуна D2 и D0,12,3 поэтому
дополнительно вычерчиваем механизм в положении
.
Начало рабочего хода приходится на участок между положениями ползуна D2 и D0,12,3 поэтому
дополнительно вычерчиваем механизм в положении ![]() ,
соответствующем началу рабочего хода. Конец рабочего хода приходится на
положение ползуна
,
соответствующем началу рабочего хода. Конец рабочего хода приходится на
положение ползуна ![]() . В качестве рабочего хода
целесообразно принимать такую часть возвратно-поступательного движения ползуна,
когда шатун CD будет работать на растяжение.
. В качестве рабочего хода
целесообразно принимать такую часть возвратно-поступательного движения ползуна,
когда шатун CD будет работать на растяжение.
Круговую циклограмму вычерчиваем в графической части курсовой работы, совмещая ее с планом положений ведущего звена. Выделяем следующие элементы движения:
|
1 |
Прямой ход |
– |
от положения кривошипа А7 до
положения А1 ( |
|
2 |
Обратный ход |
– |
от положения кривошипа А1 до
положения А7 ( |
|
3 |
Рабочий ход |
– |
от |
|
4 |
Передний перебег |
– |
от |
|
5 |
Задний перебег |
– |
от А’6 до А8
( |
2.2 Построение планов скоростей и ускорений для исследуемых положений механизма
При помощи круговой циклограммы определяем, что
рабочему ходу ползуна соответствуют положения механизма № ![]() , 3, 4, 5, 6,
, 3, 4, 5, 6, ![]() . Для
этих шести положений механизма на отведенном месте чертежа строим планы
скоростей.
. Для
этих шести положений механизма на отведенном месте чертежа строим планы
скоростей.
Угловая скорость
ведущего звена 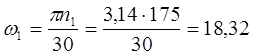 рад/с.
рад/с.
Скорость точки А
кривошипа ![]() м/с.
м/с.
Длину отрезка Pa,
соответствующего вектору ![]() на планах скоростей,
принимаем равной 70 мм. Определяем масштаб планов скоростей
на планах скоростей,
принимаем равной 70 мм. Определяем масштаб планов скоростей
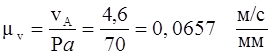 .
.
Для определения
положения точки B на планах скоростей используем векторное уравнение ![]() , где
, где ![]() . Кроме
того, известно направление вектора скорости точки В:
. Кроме
того, известно направление вектора скорости точки В: ![]() .
.
Положение
точки С на планах скоростей находим, решив графически векторное
уравнение ![]() .
.
Положение точки d
на планах скоростей определяем путем графического решения векторного уравнения ![]() , где
, где ![]() . При этом учитываем, что скорость ползуна
. При этом учитываем, что скорость ползуна ![]() всегда параллельна направляющей.
всегда параллельна направляющей.
Обозначения векторов скоростей точек и соответствующих им отрезков на плане скоростей представлены в таблице 3:
Таблица 3 – Обозначения векторов скоростей точек и соответствующих им отрезков на плане скоростей
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.