1 Задание на расчет и исходные данные
Выполнить структурный, кинематический и динамический анализ плоского шарнирно-рычажного механизма (рисунок 1.1)

Рисунок 1.1 – Кинематическая схема механизма.
Исходные
данные: ![]() мм,
мм, ![]() мм,
мм, ![]() мм,
мм, ![]() мм,
мм, ![]() мм,
мм, ![]() мм,
мм, ![]() мм,
мм, ![]() мм,
мм, ![]() мм.
мм.
Удельная масса
звеньев ![]() кг/м.
кг/м.
Частота
вращения ведущего звена ![]() об/мин.
об/мин.
Сила
сопротивления ![]() Н прикладывается к ведомому
звену (ползуну) противоположно его ходу.
Н прикладывается к ведомому
звену (ползуну) противоположно его ходу.
2 Структурный анализ механизма
Степень подвижности механизма (рисунок 2.1) определим при помощи формулы Чебышева (структурной формулы плоских механизмов):
![]() , где
, где ![]() - число
подвижных звеньев механизма,
- число
подвижных звеньев механизма, ![]() ;
;
![]() - число низших кинематических пар,
- число низших кинематических пар, ![]() (O1, O2, A, B,
C, D, E);
(O1, O2, A, B,
C, D, E);
![]() - число высших кинематических пар,
- число высших кинематических пар, ![]() .
.
![]() .
.
Механизм имеет одну степень подвижности.
Механизм образован последовательным присоединением к механизму I класса (ведущему звену со стойкой) группы Асура II класса 1-го вида, а затем группы сура II класса 2-го вида. Последовательность образования механизма представлена на рисунках 2.2-2.4.
 Рисунок
2.1 – Схема механизма с указанием подвижных звеньев и кинематических пар.
Рисунок
2.1 – Схема механизма с указанием подвижных звеньев и кинематических пар.
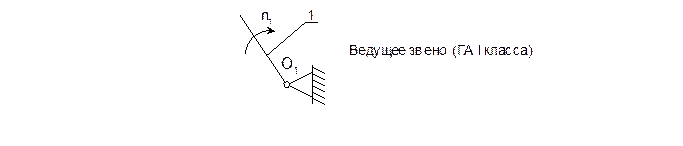
Рисунок 2.2 – Начальный механизм.
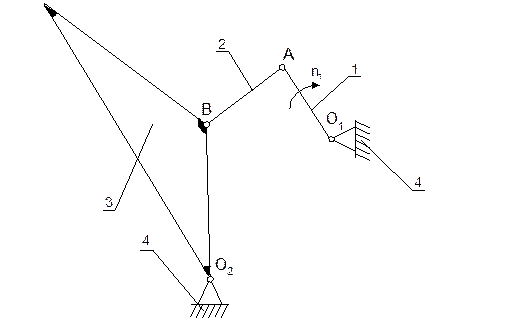
Рисунок 2.3 – Образование шарнирного четырехзвенника.
Шарнирный
четырехзвенник ![]() получен путем соединения
начального механизма и группы Асура из звеньев 2 и 3 кинематической парой
получен путем соединения
начального механизма и группы Асура из звеньев 2 и 3 кинематической парой ![]() в кинематическую цепь. Степень его
подвижности:
в кинематическую цепь. Степень его
подвижности:
![]() .
.

Рисунок 2.4 – Структурная схема шестизвенного механизма.
Формула
строения механизма: ![]() .
.
Наивысший класс присоединенных групп – второй, поэтому механизм надо отнести ко II классу.
3 Кинематический анализ механизма
3.1 Построение плана положений
План положений механизма начинаем строить с 12 положений ведущего звена. Длину отрезка О1А, изображающего на чертеже ведущее звено, принимаем равной 45 мм с целью получения оптимального масштаба плана положений. Масштаб составляет:
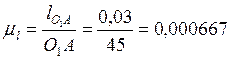 м/мм.
м/мм.
Определяем координаты шарниров и место положения направляющей, а также длины звеньев механизма на чертеже с учетом масштабного коэффициента:
![]() мм;
мм;
![]() мм;
мм;
![]() мм;
мм;
![]() мм;
мм;
![]() мм.
мм.
Аналогично определяем остальные размеры: y1=150 мм, y2=180, x1=120 мм.
В качестве нулевого принимаем такое положение ведущего звена, при котором точка А занимает крайнее левое положение. Для каждого из 12 положений ведущего звена методом засечек определяем положения всех остальных звеньев механизма.
3.2 Построение кинематических диаграмм движения ползуна
На диаграмме
перемещений по оси абсцисс откладываем отрезок ![]() мм, измеряющий
время одного оборота кривошипа, соответствующее двенадцати положениям механизма,
и двум дополнительным интервалам.
мм, измеряющий
время одного оборота кривошипа, соответствующее двенадцати положениям механизма,
и двум дополнительным интервалам.
Откладываемые
на диаграмме ![]() перемещения соответствуют перемещениям на
плане положений, поэтому и масштаб диаграммы перемещений равен масштабу плана
перемещений, т.е.
перемещения соответствуют перемещениям на
плане положений, поэтому и масштаб диаграммы перемещений равен масштабу плана
перемещений, т.е. ![]() м/мм.
м/мм.
Величину масштабного коэффициента оси абсцисс (масштаба времени) находим по формуле:
![]() с/мм.
с/мм.
В качестве начального принимаем положение 0, поскольку именно точка D12,0 является крайней на плане положений.
Для построения
диаграмм скорости и ускорения применяем метод графического дифференцирования. Величины
полюсных расстояний ![]() мм и
мм и ![]() мм выбираем
исходя из того, чтобы графики
мм выбираем
исходя из того, чтобы графики ![]() и
и ![]() соответственно поместились на местах,
отведенных им на чертеже.
соответственно поместились на местах,
отведенных им на чертеже.
Масштабный коэффициент скорости определяем по формуле:
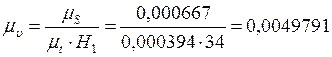
![]() .
.
Масштабный коэффициент ускорения найдем по формуле:
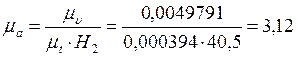
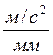 .
.
Определим скорость и ускорения ползуна 5 в девятом положении механизма:
![]() м/с,
м/с,
![]() м/с2.
м/с2.
3.3 Построение плана скоростей для исследуемого положения механизма
В качестве исследуемого выбираем девятое положение механизма. Находим величину скорости точки А звена 1:
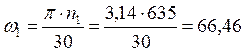 рад/с;
рад/с; ![]() м/с.
м/с.
Вектор скорости точки А изображаем в виде отрезка Pa длиной 100 мм. Определяем масштаб плана скоростей:
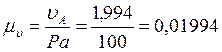
![]() .
.
Для
определения положения точки b на плане
используем векторное уравнение ![]() . В этом уравнении
известны модуль и направление вектора
. В этом уравнении
известны модуль и направление вектора ![]() , а также
направление векторов
, а также
направление векторов ![]() и
и ![]() :
: ![]() ,
, ![]() . Решая
графически уравнение
. Решая
графически уравнение ![]() , получаем точку b, определяющую величину векторов
, получаем точку b, определяющую величину векторов ![]() (отрезок
(отрезок
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.