Настройка экрана и инструментария MSExcel. Знакомство с электронными таблицами Excel. Ввод и редактирование данных в табличном процессоре Excel. Создание сводных таблиц. Подведение промежуточных итогов, страница 10

6.  Нажать кнопку ВЫПОЛНИТЬ, после чего будет осуществлена процедура поиска решения, по результатам которой выводится сообщения о найденном решении.

РЕШЕНИЕ ЗАДАЧИ ОПТИМИЗАЦИИ.

Фирма производит две модели сборных книжных полок А и В стоимостью 300 и 600 рублей соответственно. Их производство ограниченно наличием сырья (высококачественных досок) и временем работы оборудования. Для полки модели А требуется 3 м² досок, а для модели В требуется 4 м² досок. Для каждого изделия модели А требуется 12 минут  работы оборудования, а для В - 30 минут. Фирма получат от поставщиков до 1700 м² досок в неделю. В неделю можно использовать до 160 часов машинного времени.

СКОЛЬКО изделий каждой модели надо выпускать в неделю фирме для максимизации прибыли?

Сформулируем условие задачи математически, обозначив:

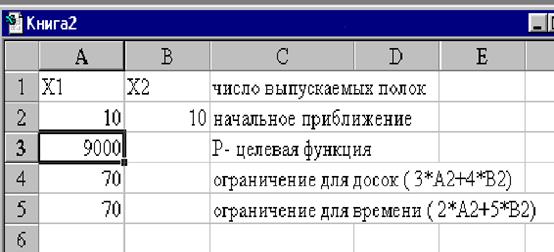
X1- число полок А;

X2- число полок В, производимых фирмой.

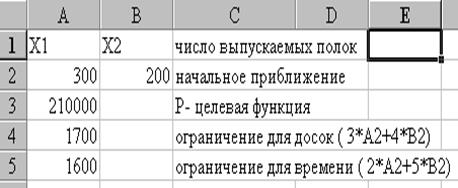
Р=300X1+600X2 - еженедельная прибыль фирмы, подлежащая максимизации (целевая функция).

Рассмотрим систему ограничений:

X1³0, X2³0 - неотрицательность числа выпускаемых полок;

3X1+4X2£1700 - ограничение на наличие досок;

2X1+5X2£1600 - ограничение на время работы оборудования (левую и правую части неравенства умножили на 10).

Решим задачу с помощью Excel, используя надстройку ПОИСК РЕШЕНИЯ.

1. Перейти на лист2 файла Оптимизация.

2. Заполним лист таблицы в соответствии с 1,2,3  пунктом порядка решения задач оптимизации.

•  Переменные Х1, Х2 (начальные приближения) расположим в ячейках А2, В2 соответственно. Это могут быть любые положительные числа, с которых компьютер начнет расчеты.

•  В ячейку А3 введем формулу целевой функции =300*А2 + 600*В2;

•  В ячейку А4 введем ограничение на наличие досок =3*А2 + 4*В2;

•  В ячейку А5 введем ограничение на время работы оборудования =2*А2+5*В2;

Выполним пункты 4 и 5 порядка решения задач оптимизации:

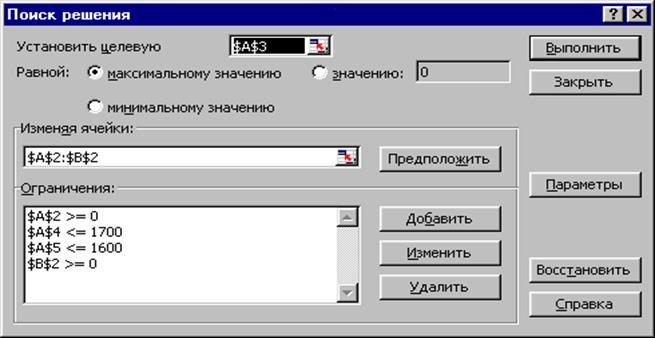
3.       Вызвать диалоговое окно СЕРВИС/ПОИСК РЕШЕНИЯ.

4.       Заполнить параметры диалогового окна:

•  Установить целевую функцию -  А3.

•  Определить тип оптимизации (искать максимум).

•  Адреса ячеек с переменными  -  $А$2:$В$2.

•  Задать систему ограничений.

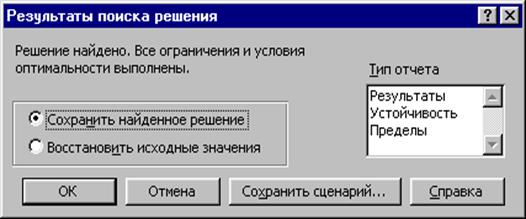
5.       Нажать кнопку ВЫПОЛНИТЬ

Полученные результаты можно сохранить или восстановить исходные значения.

 

ЗАДАЧА 1.

Фирма производит два продукта  А и В, рынок сбыта которых не ограничен. Каждый продукт должен быть обработан каждой из машин  I, II, III. Время обработки для каждого из изделия А и В соответствует таблице:

	I	II	III
А	0,5 час	0,4 час	0,2 час
В	0,25 час	0,3 час	0,4 час

Время работы машин I, II, III соответственно 40, 36, 36 часов в неделю, а прибыль от продажи изделий А и В составляет соответственно  5 и 3 доллара.

Определите недельные выпуски изделий А и В, максимизирующие прибыль. Сохранить полученные результаты.

ЗАДАЧА 2.

На новом листе решить следующую задачу. Фирме требуется уголь с параметрами качества: содержание фосфора не более 0,03% и с долей зольных примесей не более 3,25%. Доступные 3 сорта угля имеют стоимость:

Сорт угля	Содержание фосфора	Содержание золы	Цена за тонну
А	0,06%	2,0%	30
В	0,04%	4,0%	30
С	0,02%	3,0%	45

Как их смешивать, чтобы получить минимальную цену и удовлетворить ограничениям на содержание примесей. Сохранить полученные результаты.

ЗАДАЧА 3.

На новом листе решить следующую задачу. На коммерческих маршрутах А, В возникла потребность в дополнительном транспорте. На маршруте А требуется 5 доп. автобусов, на маршруте В требуется 7 доп. автобусов. Известно, что 3, 4 и 5 автобусов могут быть получены из гаражей Г1, Г2 и Г3 соответственно. Расстояние от гаражей до маршрутов А и В приведены в таблице:

ГАРАЖ	Расстояние от гаражей до маршрутов /км/
	А	В
Г1	3	4
Г2	1	3
Г3	4	2