![]()
![]() кНм;
кНм;
![]() кНм.
кНм.
Эпюра М ограничена прямой линией.
![]()
Этот участок начинается с сосредоточенного момента, т.е. на эпюре М должен быть скачок, численно равный величине этого момента.
![]() кНм;
кНм;
![]() кНм;
кНм;
Эпюра М – прямая линия.
![]()
![]() кНм;
кНм;
![]() .
.
25
Способ построения эпюры М по площади эпюры Q позволяет легко проверять эпюры моментов, построенные любым другим способом.
2.7. Способ сложения действия сил при построении эпюр Q и М.
Этот способ основан на принципе независимости действия сил, гласящем, что результат действия на конструкцию системы нагрузок равен сумме результатов воздействия каждой нагрузки в отдельности. Согласно этому принципу можно построить эпюры Q и M отдельно от каждой нагрузки, а потом координаты этих эпюр в характерных сечениях сложить алгебраически или произвести графическое суммирование.
Для стержня,
изображенного на рис. 2.9а, построим эпюры Q и M методом сложения действия сил. Построим эпюры Q и М от каждой нагрузки в отдельности упрощенным аналитическим
способом, а затем сложим алгебраические ординаты эпюр Q
и М в характерных сечениях балки. а) Строим
эпюры Q и М для балки, нагруженной только изгибающим
моментом ![]() кНм (рис. 2.9 б). Для заданной схемы
нагрузки
кНм (рис. 2.9 б). Для заданной схемы
нагрузки ![]() на всем участке,
на всем участке, ![]() ;
;
![]() кНм (чистый изгиб).
кНм (чистый изгиб).
25
б) Строим эпюры Q и М для балки, нагруженной только силой P=3кН (рис. 2.9 в).
![]() кН;
кН;![]() кНм; .
кНм; .
![]()
Эпюра Q ограничена линией, параллельной оси.
Эпюра М – наклонная прямая.
в) Строим эпюры Q и М для балки, нагруженной только равномерно распределенной нагрузкой (рис. 2.9 г).
![]() м
м
![]() кН;
кН; ![]() ;
;
![]() кНм;
кНм; ![]()
![]()
![]() .
.
Эпюра М ограничена вогнутой квадратичной параболой.
26
По рассчитанным значениям ординат Q и M для характерных сечений строим суммарные эпюры Q и М (рис. 5.7а).
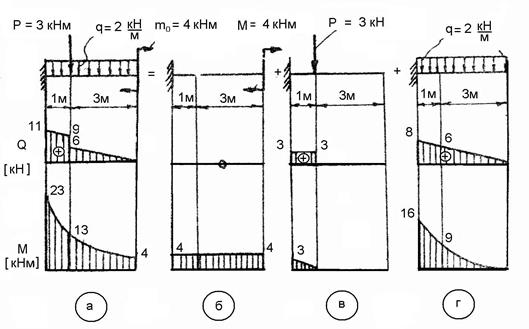
Рис. 2.9.
27
2.8. Построение эпюр в балках с шарниром.
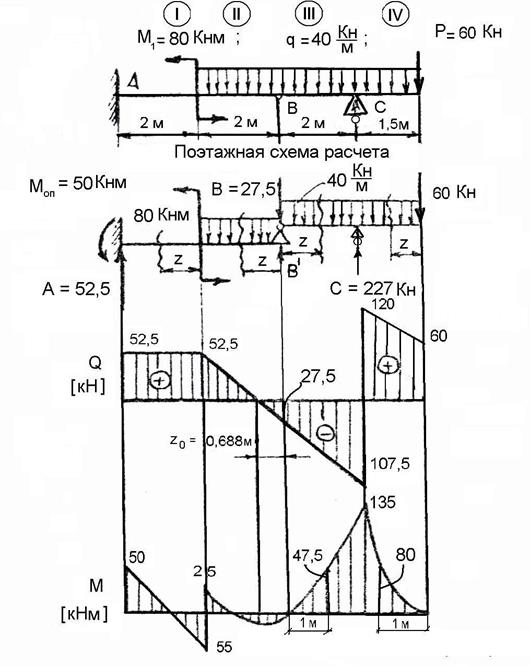
Рис. 2.10.
28
Расчет начинаем с верхнего этажа (подвесной стержень).
Определяем опорные реакции:
![]() ;
;
![]() ;
;
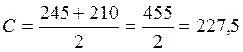 кН.
кН.
![]() ;
;
![]() ;
;
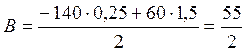 ;
;
![]() кН. (Реакция направлена вниз!).
кН. (Реакция направлена вниз!).
Проверка правильности определения реакций:
![]()
![]()
Реакции найдены верно.
Строим эпюры
![]()
![]() -
наклонная прямая.
-
наклонная прямая.
![]() кН;
кН; ![]() кН.
кН.
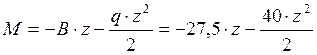 - линия 2го порядка.
- линия 2го порядка.
![]()
![]()
![]() ;
;
![]()
![]() .
.
Эпюры строятся слева направо.
![]()
![]() - линия
1
- линия
1![]() порядка
порядка
![]() кН;
кН; ![]() кН.
кН.
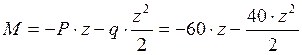 - линия
- линия ![]() порядка.
порядка.
![]() ;
; ![]()
![]() ;
;
29
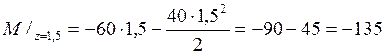
![]() .
.
Эпюры строятся справа налево.
Переходим
к расчету нижнего этажа (основной стержень). Догружаем левый стержень в точке В
усилием![]() (направленным вверх), обратным реакции в
шарнире В верхнего стержня. Идем по стержню справа налево, не определяя опорные
реакции.
(направленным вверх), обратным реакции в
шарнире В верхнего стержня. Идем по стержню справа налево, не определяя опорные
реакции.
![]()
![]() -
линия
-
линия ![]() порядка.
порядка.
![]() кН;
кН; ![]() кН.
кН.
Находим z для сечения, где М экстремален:
![]() ;
; ![]() ;
; 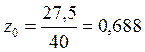 м.
м.
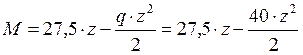 - линия
- линия ![]() порядка.
порядка.
![]() ;
; 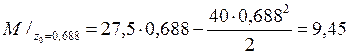
![]() ;
;
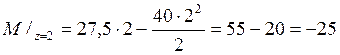
![]() .
.
Эпюры строятся справа налево.
![]()
![]() кН – const;
кН – const;
![]() - линия
- линия ![]() порядка
.
порядка
.
![]()
![]() ;
;
![]()
![]() .
.
Эпюры на участке строим справа налево.
По скачкам на эпюрах Q и M в опорном сечении А находим опорные реакции в заделке:
![]() кН (направлена вверх);
кН (направлена вверх);
![]()
![]() (действует против
часовой стрелки).
(действует против
часовой стрелки).
Внимание! В промежуточном шарнире В момент равен нулю.
30
На эпюре Q в этом сечении нет скачка (если не приложена сосредоточенная сила).
![]()
![]() .
.
![]() кН.
кН.
2.9 Построение эпюр внутренних усилий силовых факторов (Q, M, N) в плоских рамах.
Рама – это стержень с ломанной осью. Рассмотрим построение эпюр на примере плоской рамы, показанной на рис. 2.11.
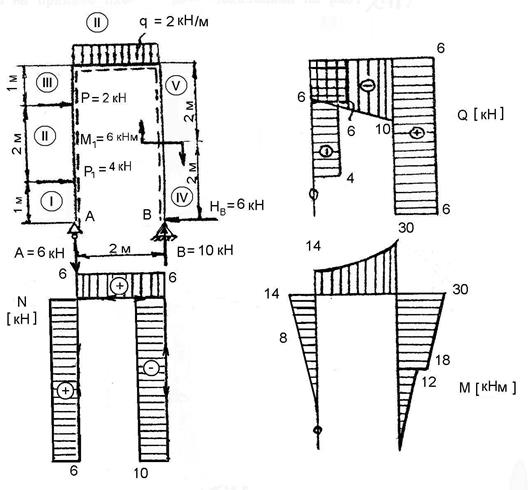
Рис. 2.11.
31
Чтобы правильно ориентироваться в знаках Q и М в рамах обычно выбирают условное нижнее волокно, которое показано на рис. 2.11 пунктиром.
Определяем опорные реакции.
![]() кН.
кН.
![]() ;
; ![]() ;
;
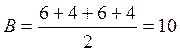 кН.
кН.
![]() ;
; ![]() ;
;
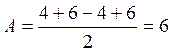 кН (Реакция направлена вниз.)
кН (Реакция направлена вниз.)
Контроль:
![]() ;
; ![]() .
.
Разбиваем раму на шесть участков и составляем для каждого участка уравнения для поперечной силы Q и изгибающего момента М.
(знаки Q и М определяем, используя условное нижнее волокно)
![]()
![]() ;
; ![]() ;
;
![]()
![]() ;
; ![]() кН – const.
кН – const.
![]() ;
; ![]() ;
; ![]()
![]() .
.
Растянуто условно верхнее волокно.
![]()
![]() ;
; ![]() кН – const.
кН – const.
![]() ;
;
![]()
![]() ;
; ![]()
![]() .
.
Растянуто условно верхнее волокно.
Эпюра М на II и III участках – прямая линия.
![]()
![]() ;
; ![]() кН – const.
кН – const.
![]() ;
; ![]() ;
; ![]()
![]() .
.
32
Растянуто условно верхнее волокно.
![]()
![]() ;
; ![]() кН – const.
кН – const.
![]() .
.
![]()
![]() ;
;
![]()
![]() .
.
Растянуто условно верхнее волокно.
Эпюра М
ограничена прямой наклонной линией; в точке, где приложена пара сил, на эпюре М
скачок, численно равный ![]()
![]() .
.
![]()
![]() - это прямая наклонная линия;
- это прямая наклонная линия;
![]() кН;
кН;
![]() кН.
кН.
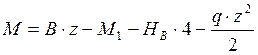 - линия
- линия ![]() порядка,
квадратичная парабола.
порядка,
квадратичная парабола.
![]()
![]() ;
;
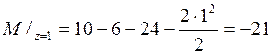
![]() .
.
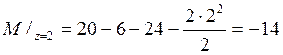
![]() .
.
Растянуто верхнее волокно.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.