Построение эпюр внутренних усилий в плоских и пространственных конструкциях: Методические указания по дисциплине «Сопротивление материалов», страница 3

Используя дифференциальные зависимости между нагрузкой и внутренними усилиями, можно строить эпюры внутренних силовых факторов упрощенным аналитическим методом.

а) при растяжении:  

б) при кручении:   

в) при изгибе:        

Эпюры строятся слева направо в направлении положительного интегрирования. При построении эпюр Q и М (при изгибе) упрощенным аналитическим методом используются также некоторые другие следствия из теоремы “о дифференциальных зависимостях”:

1. Если на участке Q положительно то М на этом участке возрастает и наоборот, если Q < 0, то М убывает.

2. Если Q проходит через нуль, меняя знак, то на эпюре М в этом сечении имеется экстремум.

3. Если Q = 0 на всем участке, то момент на этом участке постоянный, в том числе и равный нулю.

4. Так как 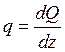, то на основании геометрического толкования производной можно считать, что тангенс угла наклона касательной к эпюре Q есть величина интенсивности нагрузки.

Следовательно, и 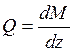 есть тангенс угла наклона касательной к эпюре М.

5. Если нагрузочная эпюра q  очерчивается линией n^го порядка, то эпюра Q – линией (n + 1) порядка, эпюра М – линией (n + 2) порядка  (следствие “о степенях эпюр”).

6. Чем больше по абсолютной величине ордината предыдущей эпюры, тем круче идет эпюра последующая (q – Q – M) (следствие “о крутизне эпюр”).

11

7. Выпуклость на эпюрах моментов, построенных со стороны растянутого волокна, всегда в сторону действующей нагрузки (“правило нити”).

8. В сечениях, где приложена сосредоточенная сила, на эпюре Q обязателен скачок на величину приложенной силы, а на эпюре моментов – излом в сторону действия силы.

9. Если в сечении балки действует пара сил (момент), то на эпюре Q это не отражается, а на эпюре М – скачок на величину момента.

1.7. Виды стержней и стержневых конструкций (Рис. 1.6)

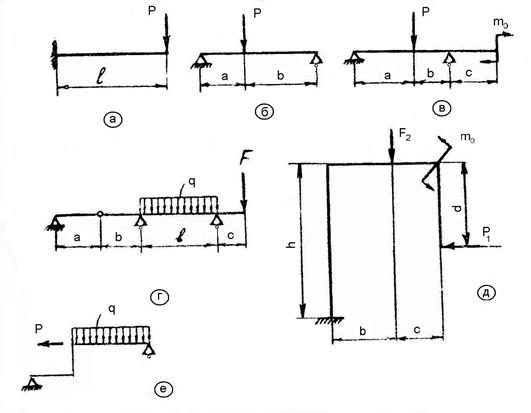
Рис. 1.6. Типы конструкций а – консольный стержень;

б – двухопорный стержень;

в – двухопорный стрежень с консолью;

г – многопролетный стержень с консолью и внутренним шарниром;

д – консольная рама или стержневая конструкция;

е – двухопорная стержневая конструкция.

12

1.8. Типы опор.

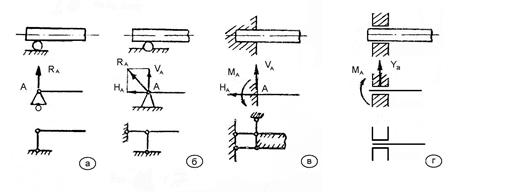
Рис. 1.7.

а – шарнирно-подвижная опора;

б – шарнирно-неподвижная опора; в – защемление или глухая заделка;

г – подвижная заделка.

Реакции опор определяют при помощи уравнений статики.

2. ПРИМЕРЫ

2.1. Построение эпюры продольных сил для вертикального стержня.

Определяем опорную реакцию из уравнения равновесия:

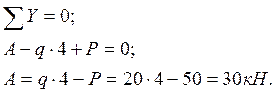
Строим эпюру N

Эпюра строится снизу вверх.

    

 - линия 1^го порядка ограничивает эпюру;

13

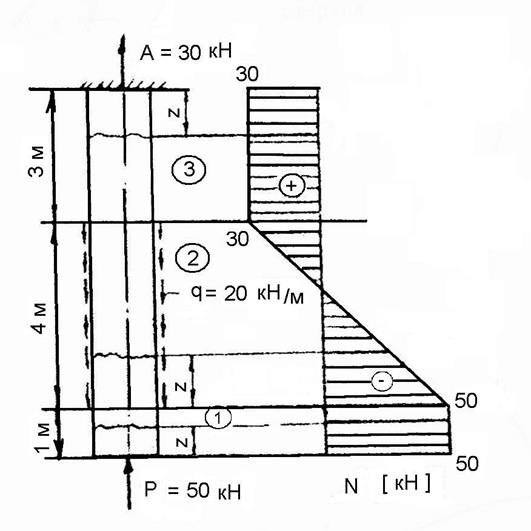
Рис. 2.1.

Эпюра строится снизу вверх.

Эпюра строится сверху вниз.

14

2.2. Построение эпюры продольных сил для горизонтального стержня.

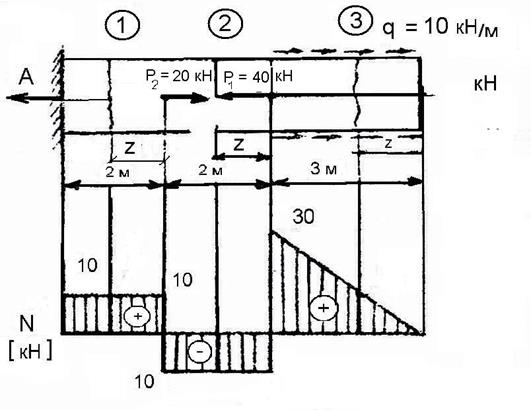
Рис. 2.2.

Опорную реакцию определять не будем.

Строим эпюру N:

    

Эпюра строится справа налево.

     .

Эпюра строится справа налево.

    

 - линия 1^го порядка  ограничивает эпюру;

15

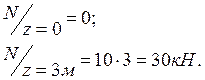
Эпюра строится справа налево.

2.3. Построение эпюры крутящих моментов для вала на двух опорах.

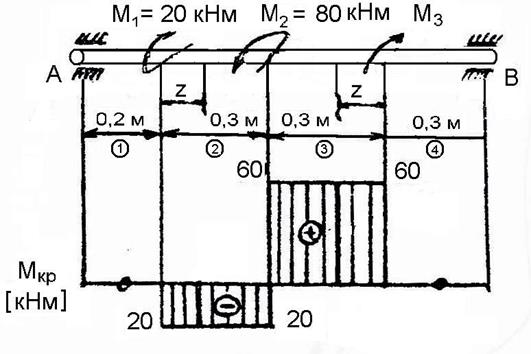
Рис. 2.3.

Из условия равновесия вала определяем неизвестный момент :

 (z – продольная ось стержня);

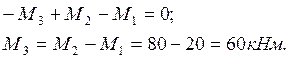
Строим эпюру .

На валу два нерабочих участка, которые сразу “зануляем”:

участки 1 и 4.

16

Эпюра строится слева направо.

м

Эпюра строится справа налево.

Скачки на эпюре в сечениях на границах участков 1,2,3 соответствуют величине действующих в этих сечениях сосредоточенных пар сил (моментов).

2.4. Построение эпюры крутящих моментов для стержня, защемленного консолью.

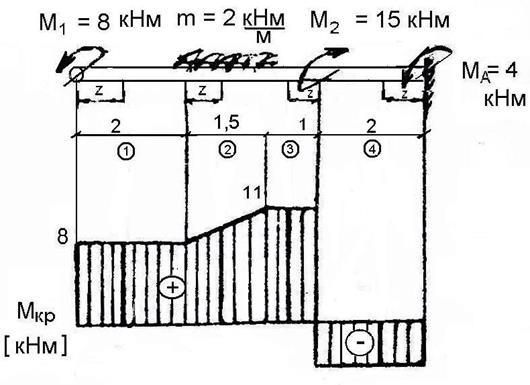
Рис. 2.4.

Реакция опоры определяется из уравнения равновесия:

17

    z – продольная ось

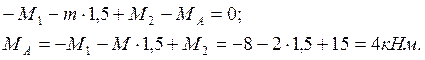
Для консольных стержней опорные реакции можно не определять, если рассматривать все участки со стороны свободного конца.

Строим эпюры:

    

Эпюра строится слева направо.

 - линия 1-го порядка ограничивает эпюру;

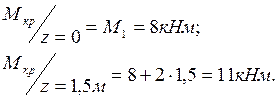
Эпюра строится слева направо.

    

Эпюра строится справа налево.

Эпюра строится справа налево.

Скачки на эпюре соответствуют действующим в сечениях сосредоточенным моментам.

2.5. Построение эпюр поперечных сил (Q) и изгибающих моментов (М) аналитическим способом.

Разберем на примере построение эпюр для стержня, находящегося под действием системы сил, расположенной в одной плоскости (Рис. 2.5).

Определяем опорные реакции из уравнений статики.

18

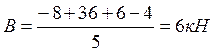
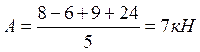
Проверка:

значит реакции определены верно.

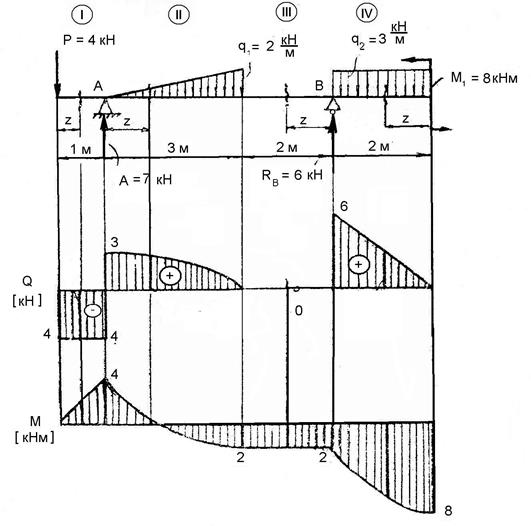
Рис. 2.5.