Построение эпюр внутренних усилий в плоских и пространственных конструкциях: Методические указания по дисциплине «Сопротивление материалов»

МИНИСТЕРСТВО ОБРАЗОВАНИЯ               РОССИЙСКОЙФЕДЕРАЦИИ

МАГНИТОГОРСКИЙ    ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ    УНИВЕРСИТЕТ    ИМ. Г. И. НОСОВА

КАФЕДРА ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ И СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ

ПОСТРОЕНИЕ  ЭПЮР  ВНУТРЕННИХ  УСИЛИЙ  В  ПЛОСКИХ  И  ПРОСТРАНСТВЕННЫХ  КОНСТРУКЦИЯХ                                 

Методические указания

По  дисциплине  «Сопротивление  материалов»          для  студентов  всех  специальностей.

МАГНИТОГОРСК

2006

Составитель: В.Н.Яременко

Построение  эпюр  внутренних  усилий  в  плоских  и  пространственных  конструкциях: Методические  указания  по дисциплине «Сопротивление материалов» для студентов всех специальностей.

Магнитогорск: МГТУ, 2006.

Рецензент: к.т.н, доцент  Макарчук  А.А..

                                                                                       Яременко В.Н.

ВВЕДЕНИЕ

Решение основной задачи сопротивления материалов сделать конструкцию достаточно прочной, но, по возможности, легкой невыполнимо без определения внутренних усилий, возникающих в этой конструкции.

Внутренние усилия возникают в любом упругом теле в ответ на действие внешних сил и являются функцией этих сил. Они представляют собой силы взаимодействия между частями или частицами одного и того же тела. Пока внутренние усилия не превышают сил сцепления между частицами тела, оно остается сплошным, целым. Когда же внутренние усилия превышают силы сцепления, тело разрушается. Следовательно, причиной разрушения любых тел, любых конструкций являются внутренние усилия, а не внешние силы.

Внутренние усилия в упругом теле определяются методом сечений, который является универсальным в механике сплошных сред. Этот метод шифруется первыми буквами операций, необходимых для определения внутренних усилий: РОЗУ (рассечь, отбросить, заменить, уравновесить). Метод сечений позволяет любую часть тела, мысленно отсеченную от всего тела, рассматривать как новое тело, находящееся в равновесии под действием приложенных к нему внешних и внутренних усилий. Он дает возможность найти лишь равнодействующую системы внутренних сил, действующих в сечении, или ее составляющие – внутренние силы, ориентированные по осям выбранной системы координат.

Определение же интенсивности внутренних сил в любой точке упругого тела требует знания закона их распределения по сечению, и, следовательно, знания того, как деформируется тело.

3

1. ВНУТРЕННИЕ СИЛЫ

1.1. Стандартное положение осей в стержнях.

Главные плоскости

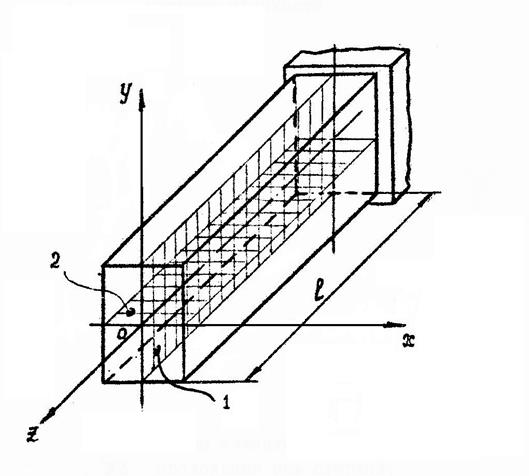
О – центр тяжести поперечного сечения, начало системы координат,

Z – продольная ось стержня,

     Х, Y – главные центральные оси  инерции поперечного сечения,

1, 2 – главные плоскости стержня.

Рис. 1.1

Стержнем называется тело, один из размеров которого (длина) много больше двух других взаимно перпендикулярных размеров.

4

Сечение стержня, перпендикулярное продольной оси, называется поперечным сечением.

Продольная ось стержня – это геометрическое место центров тяжести поперечных сечений (линия, соединяющая центры тяжести поперечных сечений). Различают стержни прямолинейные и криволинейные. В дальнейшем рассматриваем только стержни с прямолинейной продольной осью, как наиболее технологичные.

1.2. Внутренние силы.

Внутренними силами, называются силы, приложенные к центру тяжести поперечного сечения и уравновешивающие рассматриваемую часть стержня при его условном рассечении. Таким образом, внутренние силы являются условными силами, действующими в рассматриваемом сечении. Из определения следует метод определения внутренних сил – метод сечений или РОЗУ (рассечь, отбросить, заменить, уравновесить).

Известно, что уравновесить тело можно, приложив к нему (к центру тяжести рассматриваемого сечения) сосредоточенную силу и момент. Однако их ориентация в пространстве неизвестна. Удобнее разложить данную силу и момент на три взаимно перпендикулярные оси X, Y, Z. (см. рис.1.1)

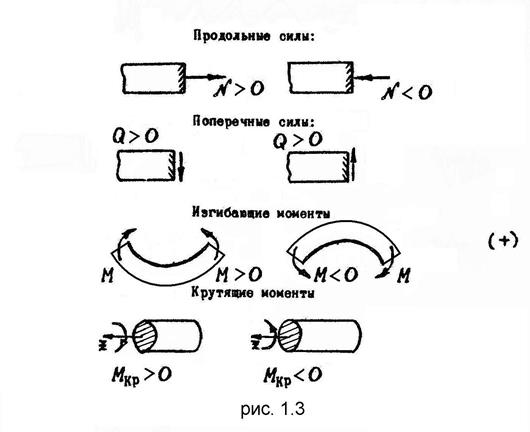
В поперечных сечениях стержней в общем случае нагружения могут действовать шесть внутренних сил (рис.1.2). Так как в общем случае существуют шесть независимых уравнений равновесия, то все шесть внутренних сил определимы. Примем следующие правила знаков внутренних сил (рис. 1.3).

Продольная сила (N) численно равна алгебраической сумме проекций всех внешних сил, лежащих с одной стороны сечения, на нормаль к сечению.

Поперечная сила (Q) численно равна алгебраической сумме проекций всех внешних сил, лежащих с одной стороны сечения, на оси Х или Y в сечении.

Изгибающий момент (М) численно равен алгебраической сумме моментов всех внешних усилий, лежащих с одной стороны сечения, относительно осей Х или Y в сечении.

Крутящий момент (М_Кр) численно равен алгебраической сумме моментов всех внешних усилий, лежащих с одной стороны сечения относительно нормали к сечению.

Если в сечении действует только продольная сила (N), то стержень испытывает растяжение (сжатие).

5

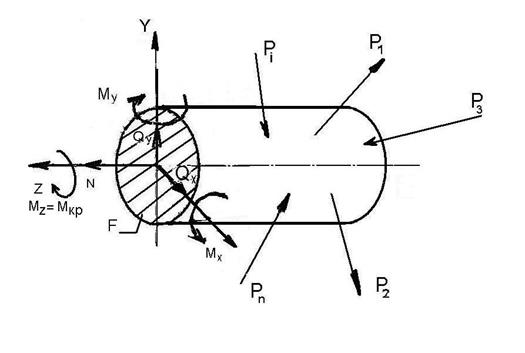
Рис. 1.2                                                 

6

Если в сечении действует только поперечная сила (Q), то стержень работает на сдвиг.

Когда в поперечном сечении стержня действуют изгибающий момент (М) и поперечная сила (Q), стержень испытывает изгиб.

Действующий в сечении крутящий момент (М_Кр) заставляет стержень работать на кручение.

Внутренние силы каким-то  образом распределяются по площади поперечного сечения. Пусть по элементарной площадке dF с координатами х, y действует продольная сила dN и поперечные силы dQ_y и dQ_x (рис. 1.4)