Построение эпюр внутренних усилий в плоских и пространственных конструкциях: Методические указания по дисциплине «Сопротивление материалов», страница 4

19

Разбиваем стержень на участки, отличающиеся характером приложенной нагрузки. Таких участков на представленном стержне – четыре.

На каждом участке законы изменения поперечной силы Q и изгибающего момента М постоянны. Составляем выражения поперечных сил и изгибающих моментов в поперечном сечении стержня на расстоянии z от начала каждого участка.

Q = - P;     М = - Р .

Исследуем полученные уравнения.

Q = - P – это уравнение содержит z⁰, значит линия, ограничивающая эпюру Q, проходит параллельно оси z.

Q = - 4 кН – const;

M = - P∙z – это уравнение прямой, поэтому достаточно знать значение момента в двух точках.

    

Наносим на 1 участок эпюры Q и М. Эпюра изгибающего момента строится на растянутом волокне, поэтому отрицательные значения момента откладывают вверх от оси, а положительные – вниз. На эпюре моментов знак не ставится.

Определим Q и М в сечении, отстоящем на расстоянии z от острого угла для нагрузки распределенной  по треугольному закону (рис. 2.6).

 

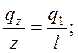
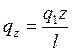
20

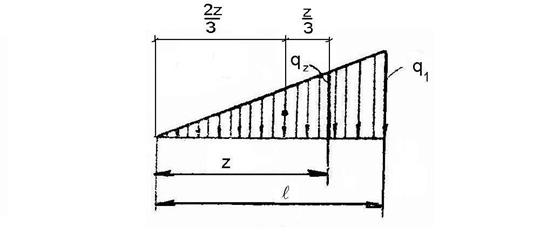
Рис. 2.6.

Составляем уравнение поперечной силы на втором участке.

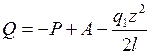 - это квадратичная парабола

l – длина второго участка;

   .

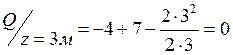Согласно дифференциальной зависимости при изгибе 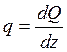 парабола,. ограничивающая эпюру Q, расположена выпуклостью вверх.

Составляем уравнение изгибающего момента для второго участка:

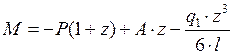 - это кубическая парабола;

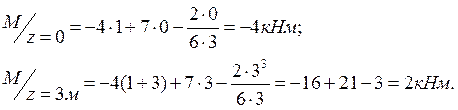
Эпюра моментов ограничена кубической параболой с выпуклостью вниз.

21

 - прямая линия;

     

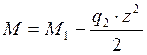 - квадратная парабола;

  

       

  

   

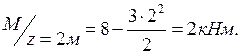
21

Анализируя эпюру Q  и М, видим, что в сечениях балки, где приложена сосредоточенная сила (или реакция, перпендикулярная оси балки), значение Q изменяется скачкообразно на величину приложенной силы. Аналогично в сечениях, где приложены сосредоточенный внешний момент (в том числе и опорная реакция в виде момента), значение изгибающего момента изменяется скачкообразно на величину приложенного момента. Линия, ограничивающая эпюру М, на порядок выше линии, ограничивающей эпюру Q. На участке, где Q = 0 (участок III), величина изгибающего момента постоянна.

2.6. Построение эпюр Q и М упрощенным аналитическим способом.

Этот способ основан на следствиях из дифференциальных зависимостей при изгибе между q, Q и М

               

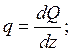
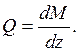
Подробно эти зависимости рассмотрены ранее (см. раздел 1.6).

Для нахождения значений поперечной силы и изгибающего момента упрощенным аналитическим способом необходимо знать площади  ряда фигур. Справочный материал по наиболее часто встречающимся эпюрам моментов приведен на Рис. 2.7.

22

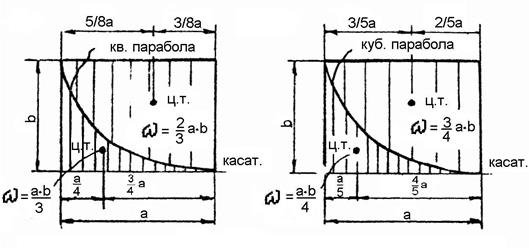
Рис. 2.7.

Для балки, приведенной на Рис. 2.8, построим эпюры Q и М упрощенным аналитическим способом, т. е. не составляя аналитических выражений для Q и М, ограничиваясь вычислениями значений поперечных сил и изгибающих моментов в характерных сечениях балки и используя выводы из дифференциальных зависимостей.

1. Определяем опорные реакции

 ;

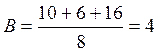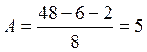 кН.

 ;

 кН;

 

Реакции определены верно.

При построении эпюр Q и M упрощенным аналитическим способом идут в направлении положительного интегрирования,

т. е. слева направо, тогда сосредоточенной  внешней силе или реакции, направленным вверх, будет соответствовать скачок на эпюре Q, направленный вверх.

23

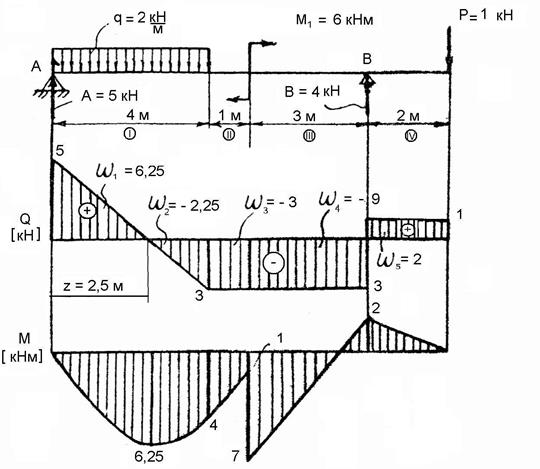
Рис. 2.8.

Разбиваем балку на четыре участка и сначала строим эпюру Q, рассуждая следующим образом. На первом участке, который начинается с опоры А, в начале имеется скачок, числено равный величине реакции А = 5 кН. Далее Q уменьшиться по закону прямой на величину грузовой площади распределенной нагрузки q, действующей на I участке. Тогда

кН;

кН.

На втором и третьем участках величина Q не меняется  (наличие не влияет на эпюру Q). Четвертый участок начинается опорной реакцией кН, направленной вверх, следовательно,

24

кН. Как и на 3 участке эпюра проходит параллельно оси (z).

Строим эпюру изгибающего момента, для чего предварительно закрепляем сечение, в котором Q = 0. (Можно из подобия треугольников, можно из уравнения  ; м.) Вычисляем площадь эпюр Q на каждом участке: кНм; кНм; кНм;   кНм;   кНм. (При подстановке этих значений в формулу «площадей» будем учитывать знак.)

         

; кНм;

кНм.

На первом участке эпюра М ограничена квадратичной параболой, направленной выпуклостью вниз. В сечении, где , т.е. при м, изгибающий момент достигает экстремального значения ( кНм).