ВВЕДЕНИЕ
Знакомство с современной физикой, в отличие от физики классической, вызывает естественные трудности восприятия основных понятий и идей квантовой механики - этого совершенно нового способа описания состояния микрочастиц и динамических законов, управляющих их движением.
Законы квантовой механики составляют основную теоретическую базу в изучении строения вещества. Так, опираясь на них, удалось выяснить строение атомов, установить природу химической связи, объяснить периодическую систему элементов, понять строение атомных ядер и свойства элементарных частиц.
Трудности при знакомстве с основами квантовой механики начинаются уже с описания основных характеристик самой микрочастицы, ее физического состояния, и, вообще, возможности задания ее начального и текущего состояния и контроля изменения этого состояния в процессе взаимодействия частицы с окружающими ее телами.
Даже сама возможность использования таких, казалось бы очевидных понятий, как пространственное положение микрочастицы, его изменение во времени, движение по траектории - для микрочастицы становится проблематичной. Более того, возникает существенное, неожиданное осложнение, связанное с взаимодействием микрочастицы с контролирующим ее движение измерительным прибором. Если в классической физике молчаливо предполагалось, что этим влиянием можно пренебречь, то в квантовой механике, как оказалось, воздействие прибора на микрообъект может радикально изменить его состояние.
Поэтому в теоретическую ткань квантовой механики органично вплетена взаимосвязь величин, характеризующих сами микрочастицы, с физическими величинами, непосредственно измеряемыми приборами.
Настоящая работа, позволит студенту более наглядно познакомиться с удивительными свойствами микрочастиц при их движении и взаимодействии с силовыми физическими полями в самых простых модельных ситуациях.
В процессе подготовки к выполнению работы и при ее непосредственном выполнении студенты приобретают необходимые первоначальные навыки и представления об основных понятиях и этапах решения типичной квантово-механической задачи.
На примере простейших барьерных задач в работе проводится компьютерное моделирование поведения микрочастицы в силовых полях с прямоугольным потенциалом (типа потенциальной ступени или барьера.)
С этой целью вначале студенту предлагается просмотреть демонстрационную программу, в которой моделируется поведение микрочастицы в зависимости от ее массы и энергии и от изменения силового поля, действующего на микрочастицу.
Можно наблюдать, как при варьировании энергии и массы закономерно меняются амплитуды отраженной и проходящей волн и, что особенно важно, наблюдать типичный квантово - механический эффект - эволюцию осциллирующих функций в экспоненциальные волновые, что соответствует некоторой глубине проникновения Xmax частицы в классически недоступную область.
Прочувствовав механизм возникновения туннельного эффекта, далее, в основной программе, студент уже самостоятельно на примере конкретного задания анализирует изменение состояния частицы и ее движение в двух вариантах силовых полей:
- Потенциальный скачок (ступенька)
- Потенциальный барьер.
В конце работы студент должен графически проанализировать изменение коэффициентов отражения (R) и прохождения (Т), а для случая потенциального барьера, кроме того, провести графический анализ вероятности просачивания сквозь него (D1) в зависимости от ширины барьера - L, массы частицы - mas и энергии частицы (U0-E).
1 Основные положения, касающиеся движения микрочастиц в потенциальных полях
1.1 Квантово-механическое описание движения частиц в одномерном случае
Рассмотрим одномерный случай.
Тогда динамическое уравнение, решения которого определяют движение микрочастицы, запишется:
|
|
(1) |
где
![]() (x,t)
- волновая функция, описывающая состояние микрочастицы;
(x,t)
- волновая функция, описывающая состояние микрочастицы;
m, кг - ее масса;
h - постоянная Планка;
![]()
U(x,t) - потенциал силового поля, действующего на частицу.
В алгебре решением уравнения называют числа - корни уравнения, которые будучи подставленными в уравнение, обращают его в тождество. Решением дифференциального уравнения называют функцию, которая будучи подставленной в уравнение со всеми своими производными, также обращает его в тождество.
В случае постоянства потенциала решение уравнения (1) имеет вид волн де-Бройля.
|
|
(2) |
где импульс частицы:
|
|
(3) |
А и В произвольные постоянные, которые ищутся из граничных условий. В решении (2) первое слагаемое представляет собой волну, распространяющуюся вправо, а второе - волну, бегущую влево.
Далее рассмотрим два типичных случая движения микрочастицы в поле прямоугольного потенциала.
1.1.2 Потенциальный скачок
Низкий потенциальный скачок ( см. Рисунок 1).
В этом случае энергия частицы больше высоты потенциального скачка (E>U).
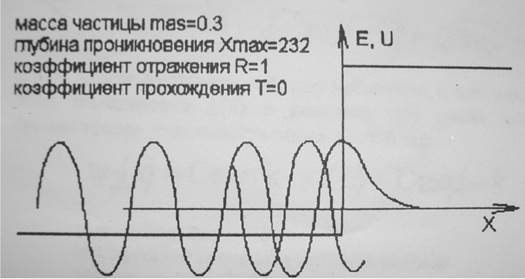
Рисунок1 - Решение уравнения Шредингера для случая высокой потенциальной ступеньки
Для стационарного случая (независимости физической ситуации от времени) решение уравнения Шредингера
|
|
(4) |
в соответствии с выражением (2) будет представлено для области слева от х=0 суммой падающей волны и отраженной:
|
|
(5) |
Здесь в отсутствие силового поля в первой области (U=0) согласно (3)
![]()
В области справа от x=0 решение будет представлено амплитудой прошедшей волны:
|
|
(6) |
Где
|
|
(6a) |
Для того, чтобы задача имела конкретно
завершенный вид и имела четкий физический смысл, необходимо в решениях (5-6)
найти неопределенные коэффициенты А, В и С. Для нахождения этих коэффициентов
используют аксиоматические свойства волновой функции ![]() (x):
(x):
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.