Основные положения, касающиеся движения микрочастиц в потенциальных полях, страница 3

С тем, чтобы удовлетворить свойству конечности волновой функции на бесконечности, очевидно коэффициент С в решении (13) необходимо выбрать равным нулю:

С=0

3)   для определения оставшихся произвольных постоянных А, В и D снова нужно использовать свойство непрерывности волновых функций, т. с. опять провести операцию «сшивания»:

После корректно проведенной операции можно получить выражения для амплитуд волны падающей А и отраженной В:

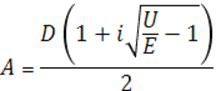
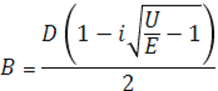
Коэффициент  отражения,  как отношение интенсивностей отраженной волны В и падающей волны А запишется в виде равенства:

Анализ решения

Таким образом, уравнение (16) приводит к выводу, что частица полностью отражается на скачке потенциала, квантово - механический вывод совпадает с классическими прогнозами. Однако здесь появляется и нечто новое, что было неизвестно в классической физике.

Решение (15) предсказывает проникновение экспоненциально спадающего слагаемого волновой функции в классически недоступную область x>0, а это означает, что микрочастица все-таки попадает на некоторое время в эту область. Затем, все же, силы поля заставляют частицу повернуть вспять и присоединиться к отраженному потоку частиц.

Такая парадоксальная ситуация. - попадание частицы в область, где ее кинетическая энергия отрицательна, возникает только в нашем восприятии. Задумаемся над возможностью разделения полной энергии частицы на слагаемые кинетическую и потенциальную.

В классической физике мы ни разу не встречались с такой проблемой и, если эго предположение привело к парадоксу, то чисто формально логически приходится согласиться, что разделять полную энергию микрочастицы на составляющие бывает не всегда корректно.

1.1.3 Прямоугольный потенциальный барьер

Силовое поле, представленное на Рисунке 2, называется потенциальным барьером высоты U₀ и ширины L.

Рассмотрим задачу о движении частицы слева и падении ее на барьер.

 Пусть барьер будет высоким: энергия Е частицы меньше высоты барьера Е<U₀.

Как утверждает макроскопический опыт, поток частиц в этом случае должен полностью отражаться. Однако, теперь  можно ожидать, что установленный выше факт проникновения микрочастиц в классически недоступную область, должен привести к физически важным результатам. Методика решения задачи в этом случае включает следующие этапы, причем теперь область пространственной координаты разбивается на три части:

1)  до границы раздела, где -∞< X< 0   уравнение Шредингера (4) остается таким же с U=0, поэтому такими же остаются и решения (5)

2)  для области высокого потенциала  0<X<L, где (E-U)<0, в уравнении Шредингера второе слагаемое снова меняет знак. И если сделать уже знакомую замену обозначений в выражении (6а):

С тем, чтобы сохранить и форму уравнения, и его решение прежним, то после этой подстановки (18) в решение (5) снова получим решение в виде суммы теперь уже вещественных экспонент:

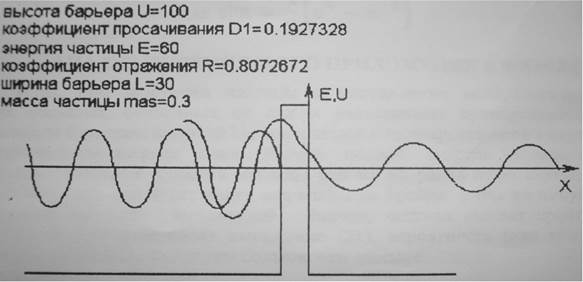
Рисунок 2 - Решение уравнения Шредингера для потенциального барьера конечной ширины

3)  справа от барьера, где х>L, частиц, идущих к барьеру нет, там могут быть только частицы, идущие со стороны барьера вправо. Волновая функция в этой области, как решение уравнения должна быть следующей:

Для определения произвольных постоянных А, В, С, D и F снова нужно использовать свойство непрерывности волновых функций, т.е. опять провести операцию «сшивания» на границе х=0:

и на границе x=L: