Основные положения, касающиеся движения микрочастиц в потенциальных полях, страница 4

Используя выражения для волновой функции (17), (19) и (20), можно подучить выражения для амплитуд волны падающей А и отраженной В, выраженных через амплитуду волны прошедшей F:

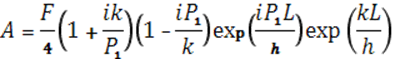
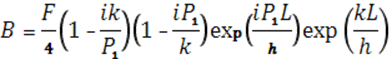
Самой интересной особенностью решения этой задачи является возможность найти отношение интенсивности прошедшей волны F к интенсивности падающей А, т.е. коэффициент прозрачности (проницаемости) D1

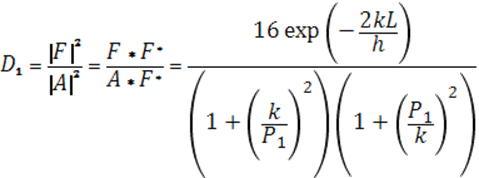
коэффициента прозрачности D1 уже легко получить выражение через энергии: здесь F^* и А^* соответствующие комплексно сопряженные величины.

Отсюда для

Можно показать, что коэффициент отражения, как отношение интенсивности отраженной волны В к интенсивности падающей А, сводится к следующему выражению:

где shx=(e^x-e^-x)

Анализ решения и его приложения в физике

Итак, при движении частицы в направлении поля, составленного из двух областей, свободных от сил и разделенных прямоугольным потенциальным барьером высотой U₀, мы пришли к выводу, что даже в случае, когда потенциальная энергия поля больше полной энергии частицы (высокий барьер) - волновая функция частицы все же не равна нулю внутри барьера. Справа от него она будет иметь вид волны де-Бройля с тем же импульсом, но с гораздо меньшей амплитудой. Значит, частица сможет пройти сквозь барьер. И, как показывает выражение (21), вероятность (или коэффициент проникновения) D₁ будет тем больше, чем меньше

-  ширина L  барьера;

-  высота барьера (разность потенциальной и полной энергии частицы)

(U.-E);

-  масса микрочастицы m.

Если в классической физике частица в этом случае не может проникнуть во внутреннюю область барьера без подкачки необходимой дополнительной энергией, то в квантовой механике возникает новое характерное явление проникновения (просачивания) частицы сквозь потенциальный барьер, и этот типично квантово-механический эффект называют «туннельным» эффектом.

Этот замечательный эффект дает объяснение самым различным природным  явлениям:

- исторически впервые, туннельный эффект был использован для объяснения явления а-распада - вылета из радиоактивных ядер а- частиц (ядер гелия);

- поистине вселенские масштабы принимает этот эффект в термоядерных реакциях, протекающих на звездах. Здесь, при температурах в десятки и сотни миллионов градусов, основная масса реагирующих ядер преодолевает электростатическое (кулоновское) отталкивание и сближается на расстояния порядка действия ядерных сил в результате этих (туннельных) подбарьерных переходов. Это и является необходимым условием начала синтеза легких ядер и выделения колоссальной энергии;

- возможность туннельных переходов дает объяснение и основу модели свободного электронного газа в кристаллах проводников;

-  туннельный переход объясняет также автоэлектронную эмиссию - явление вырывания электронов из металла сильным электрическим полем;

-  этот эффект объясняет контактные явления в металлах и полупроводниках;

-  возможность туннелирования сверхпроводящей компоненты электронов через тонкие диэлектрические слои объясняет также эффект Джозефсона в сверхпроводниках;

-  этим же эффектом очевидно можно объяснить и легкую подвижность р-электронов в системе сопряженных связей в молекулах органических соединений;

-  с туннельным эффектом связано и аномальное течение химических реакций переноса протонов, наблюдаемое при низких температурах;

-  этим же эффектом определяется аномально высокая подвижность протонов, проявляющаяся в высоких значениях чисел переноса в растворах электролитов;

-  предиссоциация реагирующих молекул также непосредственно связана с туннельным эффектом.

Данный эффект используется в нанотехнологиях, а именно в сканирующих микроскопах.