Определение периодичности диагностирования элемента автомобиля

1. Определение периодичности диагностирования элемента автомобиля.

1.1.Расчет числовых характеристик массива значений наработки

на отказ элемента автомобиля

Массив измеренных значений наработок на отказ узла автомобиля, тыс. км. (всего 60 значений)

Значительно упростить и ускорить вычисления можно путем использования преобразования результатов наблюдений (совокупности значений t_i)в статистический ряд. С этой целью весь диапазон наблюдаемых значений Т делят на m интервалов или «разрядов» и подсчитывают число значений m_i, приходящихся на каждый i-й разряд. Для этого сначала выявляется наименьшее t_min и наибольшее t_max значение элементов выборки. Зона рассеивания определяется как разность между этими значениями. Вычисленная зонарассеивания делится на равное количество интервалов, которое в зависимости от объема выборки берется как целое число, ближайшее к значению r.

По формуле Стьюдента определяем количество:

                                               (1)

и ширину интервалов для построения гистограммы:

                                                     (2)

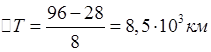
где t_max,t_min− наибольшее и наименьшее значение в массиве данных;

N – количество значений в массиве.

В таблице 1 указаны результаты систематизации в виде статистического ряда 60 значений случайной величины, распределенной на интервале [65·10³ч; 140·10³ч] при условии, чтоΔТ = 9,4·10³ч, r = 8.

Заполнять таблицу несложно. Последовательно просматривая массив значений {t_i}, оценивают, к какому разряду относится каждое число. Факт принадлежности числа к определенному разряду отмечают чертой в соответствующей строке таблицы. Затем подсчитывают n₁, …, n_i,…, n_m -число попаданий значений случайной величины (число черточек) соответственно в 1-й, …, i-й,…, m-й разряд. Правильность подсчетов определяют, используя следующее равенство:

Таблица 1 – Результаты расчетов числа попаданий в каждый интервал и статистической вероятности отказа

Статистическая вероятность q_iпопадания случайной величины на

i-й интервал рассчитывается как:

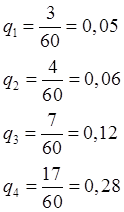
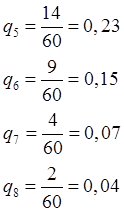
Подсчитав значения q_iдля всех интервалов и проверьте правильность расчетов, используя выражение:

Для вычислений среднего значения случайной величиныТ непосредственно по ее выборочным значениям t₁, t₂, …, t_i, …, t_Nиспользуют формулу:

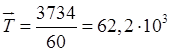
Можно для расчета среднего значения случайной величины в качестве «представителя» всех ее значений, принадлежащих i-му интервалу, принимать его середину . Тогда средняя наработка до отказа определяется как:

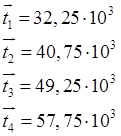
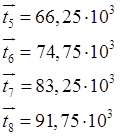
Расчет с использованием формулы (7) вносит некоторую методическую ошибку. Однако ее значение обычно пренебрежимо мало. Эту ошибку врасчетах оцениваем по формуле:

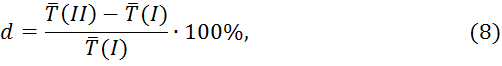
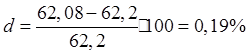
где (I) и (II) - средние значения, вычисленные соответственно с использованием формул (6) и (7).

В курсовой работе выдвинута гипотеза о том, что приведенные наработки на отказ элементов автомобилей, описываются нормальным законом распределения.

Числовыми характеристиками (параметрами) случайной величины называются характеристики наиболее существенных особенностей закона распределения. Параметры характеризуют центр распределения, масштаб иформу кривой распределения.

Наиболее часто используемыми характеристиками случайной величины, используемыми в теории надежности, являются:

– математическое ожидание (среднее значение) ;