![]()
Вычисляется величина:
![]()
![]()
Задаемся доверительной вероятностью:
![]()
что отклонение Fэ(ti)
от F(ti) будет меньше табличной величины![]() (таблицаА.3 приложения),
установленной для доверительной вероятности
(таблицаА.3 приложения),
установленной для доверительной вероятности ![]() .
Еслиуравнение (28) переписать в виде:
.
Еслиуравнение (28) переписать в виде:
![]()
и вычисленная вероятность ![]() получается незначительной (меньше
0,1), то отклонение эмпирической функции распределения от теоретической
неслучайно. Иначе говоря, Fэ(ti) плохо
согласуется с F(ti). Если же разность
получается незначительной (меньше
0,1), то отклонение эмпирической функции распределения от теоретической
неслучайно. Иначе говоря, Fэ(ti) плохо
согласуется с F(ti). Если же разность ![]() велика (больше 0,3−0,4), то
расхождение между Fэ(ti) и F(ti)
считается несущественным и гипотеза о функции распределения считается
согласованной с экспериментальными данными.
велика (больше 0,3−0,4), то
расхождение между Fэ(ti) и F(ti)
считается несущественным и гипотеза о функции распределения считается
согласованной с экспериментальными данными.
Определение согласия данных по критерию Пирсона χ2
Широкое применение критерия χ2 обосновывается легкостью его использования для проверки согласия любого распределения.
Первоначально определяется вероятность попадания значений случайной величины в каждый интервал:

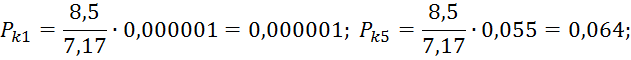
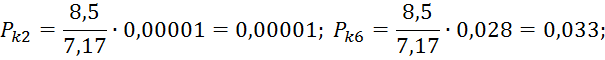
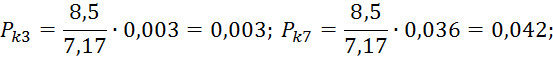
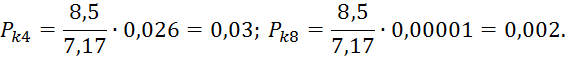
Находим значения критерия согласия Пирона для каждого интервала:
![]()
![]()
![]()
![]()
![]()
Значение критерия согласия Пирсона для всей выборки:

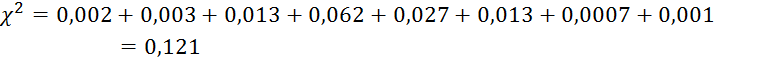
Чем меньше полученное значение χ2 , тем лучше согласие между эмпирическим и теоретическим распределением.
Определяем число степеней свободы:
![]()
где r – число параметров теоретической функции распределения, для нормального закона r = 2;
k - число интервалов.
![]()
После вычисления χ2 задаемся доверительной вероятностью γ (γ=0,2…0,3) того, что величина χ2, полученная в результате случайных отклонений частот эмпирического распределения от соответствующих частот теоретического распределения будет меньше табличного значения (χ2*), установленного для выбранной доверительной вероятности γ.
Если вычисленное значение χ2 будет меньше (χ2*), то для принятойдоверительной вероятности g гипотеза о согласии эмпирического и теоретического распределения не отвергается, в противном случае ее необходимопроверять дальше. Если вычисленное значение χ2> (χ2*) необходимо сравнить фактические частоты попадания в интервалы сожидаемыми, чтобы увидеть, какие интервалы оказывают наибольшее влияние на величину χ2. Этосравнение наглядно показывает характер отклонения от принятой теоретической модели.
3.4 Определение периодичности диагностирования поминимуму суммарных эксплуатационных потерь
Метод определения периодичности диагностирования по заданной вероятности безотказной работы применим тогда, когда имеется статистика,характеризующая наработку на отказ данного узла для группы автомобилей,а распределение отказов подчиняется какому либо закону. Когда нет возможности определить закономерность изменения технического состояниярассматриваемого элемента, а такой случай возможен при эксплуатации автомобилей в АТП, применяется метод определения lд при дискретных значениях диагностического параметра. При данном методе оптимизацию lд производят по минимуму суммарных эксплуатационных потерь Пэ. Эти потериопределяются стоимостью всех диагностических проверок, а также дополнительными затратами, связанными с несвоевременным обнаружением неисправностей.
Математическое ожидание этих потерь можно описать уравнением:
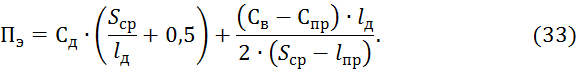
где Сд= 200 - затраты на диагностирование;
Св= 800 -восстановление отказа;
Спр= 300-предупредительное обслуживание или ремонт соответственно;
Sср – средняя наработка на отказ;
Lд– периодичность диагностирования;
Lпр– средняя периодичность предупредительного обслуживания или ремонта(для легковых автомобилей (узлы, влияющие на безопасность движения) lпр = 4000 км).
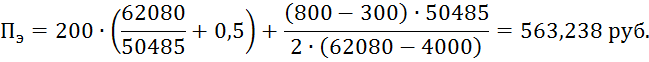
Минимизируя данную функцию, определяем оптимальное значение lд:
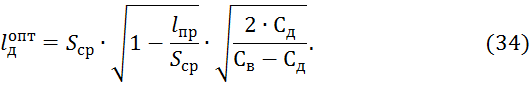
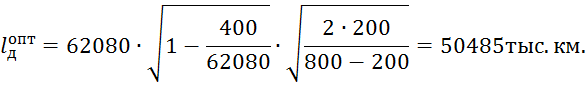
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.