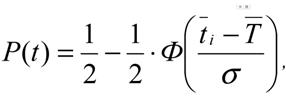Определение периодичности диагностирования элемента автомобиля, страница 4

где Ф - функция Лапласа, обладающая свойствами Ф(-х) = -Ф(х) . Табулированные значения функции Лапласа представлены приложении 1.

Вероятность восстановления определяется по формуле :

Интенсивность отказов или восстановления:

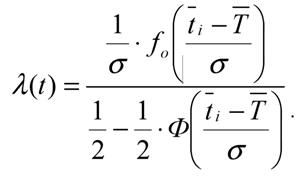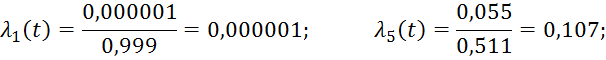
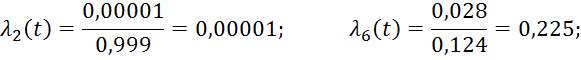
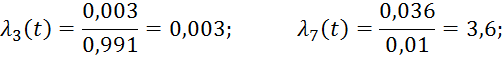
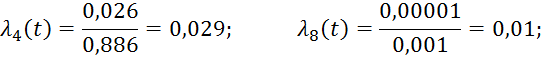
Для облегчения расчетов и проверки результатов, полученные данные сводятся в таблицу 3.

Таблица 3 - Последовательность вычислений при проверке принадлежности данных нормальному закону

3.3 Проверка гипотезы о принадлежности опытных данных к

выбранному закону распределения случайных величин

При аппроксимации эмпирических данных возможны случаи, когдаодни и те же данные могут быть одинаково успешно описаны несколькимираспределениями. Поэтому необходима проверка согласия между распределением случайной величины, полученной по результатам наблюдений спредполагаемым теоретическим распределением этой величины. Всегдапредпочтительнее выбирать то распределение, которое дает наибольшую вероятность согласия.

Решение этой задачи основано на использовании фундаментальногоположения математической статистики, согласно которому эмпирическаяфункция распределения сходится по вероятности ктеоретической при неограниченном увеличении размера выборки, если выборка принадлежит рассматриваемому теоретическому распределению.

Проводим проверку принадлежности массива опытных данных к выбранному закону распределения по критериям согласия Колмогорова, Пирсона и Романовского.

Определение согласия данных по критерию Колмогорова

Максимальное отклонение функции эмпирического распределения отфункции теоретического обозначается D_n:

Для нахождения максимального отклонения расчеты необходимо представить в виде таблицы:

Таблица 4 - Последовательность расчета максимального отклонения