Определение периодичности диагностирования элемента автомобиля, страница 2

– дисперсия D или среднее квадратическое отклонениеσ;

– коэффициент вариации V(t);

– медиана М_е и мода М_о.

Дисперсия, среднее квадратическое отклонение и коэффициент вариации показывают, насколько тесно сгруппированы возможные значения случайной величины около ее математического ожидания, т. е. характеризуют степень разброса или рассеивания.

Дисперсия непрерывной случайной величины находится по формуле:

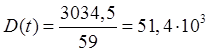
Среднее квадратическое отклонение:

В относительных единицах рассеивание выражается коэффициентом вариации:

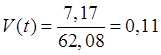
По значению коэффициента вариации можно сделать предварительные выводы о законе распределения случайных величин. Если значение V(t)≤0,3, можно выдвинуть гипотезу о том, что рассматриваемые наработки на отказ  описываются нормальным законом распределения.

 Функция распределения

Во многих практических задачах надежности вместо вероятности того,что случайная величинаТ принимает вполне определенное значение t, достаточно знать вероятность того, что случайная величина T меньше или равна t.

Эта вероятность задается интегральной функцией распределения:

Функция распределения F(t) представлена на рисунке 2. При построении и ее исследовании необходимо учитывать следующие ее свойства:

1. Вероятность того, что значение случайной величиныТ заключенной в интервале t и t+Δtравна разности функции распределения, вычисленных в точках t и t+Δt,

P(t<T≤ t+ Δt) = F(t+ Δt) - F(t).                            

2. F(t) всегда неотрицательная функция F(t)0для всех t.

3. Вероятность не может принимать значения больше 1, поэтому

0 ≤F(t) ≤ 1.                            

4. Функция распределения F(t) − неубывающая функция, т. е. при t+Δt>t

F(t + Δt) ≥F(t) .

5. При t= - ∞ функция распределения равна 0, а при t= ∞ функция распределения равна 1.

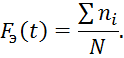
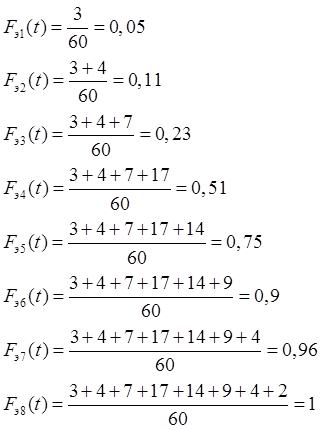
Функция плотности распределения

Наглядное представление о характере распределения непрерывной случайной величины в окрестностях различных точек дает особая функция, называемая плотностью распределения вероятности, или плотностью распределения f(t) (рисунок 3).

Предел отношения вероятности попадания непрерывной случайной величины на элементарный участок от t до t + Δtк его длине Δt, стремящейся к нулю, называется плотностью распределения случайной величиныТ вточке t:

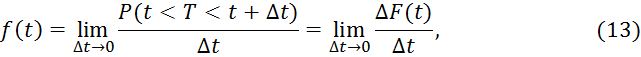
т.е.

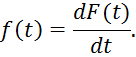
Следовательно, плотность распределения равна производной от функции распределения непрерывной случайной величины.

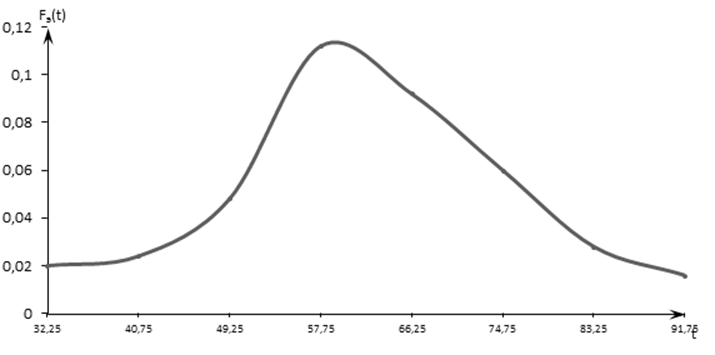
          Рисунок 1 - Функция плотности распределения

                          

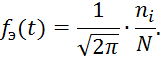
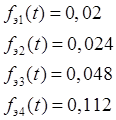
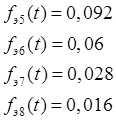
Плотность распределения, как и функция распределения, - одна изформ задания закона распределения. Она обладает следующими основнымисвойствами:

1. Плотность распределения - функция неотрицательная:

f (t) ≥ 0 для всех t.

2. Функция распределения непрерывной случайной величины равна интегралу от плотности распределения на участке от -∞ до t:

3. Вероятность того, что случайная величинаТ попадает в интервал между t и t+Δt, равна относительной площади под кривой f(t) между точками t и t+Δt, т. е.:

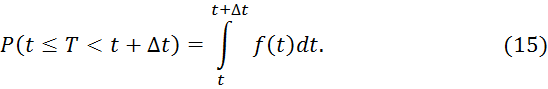
4. Интеграл в бесконечных пределах от плотности распределенияравен единице:

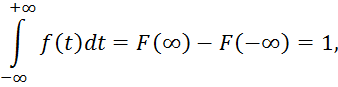
т. е. площадь, ограниченная кривой плотности распределения и осью абсцисс, равна единице.

5. Плотность распределения вероятности имеет размерность обратную размерности случайной величины:

[f(t)] =1/[t].

Заданные в курсовой работе данные по наработке элемента автомобиля являются результатом наблюдений и сбора статистических данных. Поэтому первоначально определяем эмпирические значения интегральной функции и функции плотности распределения.

Эмпирическое значение интегральной функции распределения:

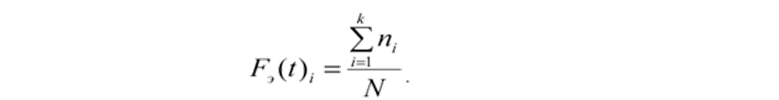
Функция плотности распределения: