Определение периодичности диагностирования элемента автомобиля, страница 3

Полученные для каждого интервала значения этих функций сводятся в таблицу 2.

Таблица 2 - Значения эмпирических значений функций F_э(t) и f_э(t)

После заполнения таблицы построить графики функций F_э(t) и f_э(t).

На графиках необходимо отметить значения моды и медианы.

        Построение теоретической функции распределения.

                         

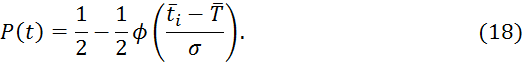
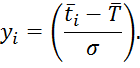
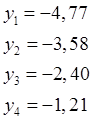
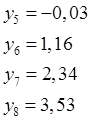
Полученные значенияу_iиспользуем для получения  с помощью таблицы значений функции .

  Построение функции плотности.

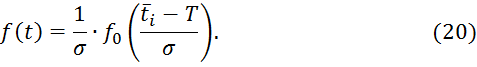
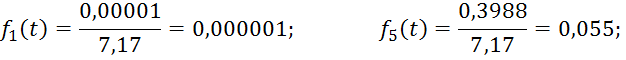
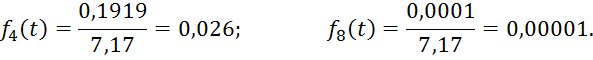
Медиана и мода случайной величины

Центр распределения непрерывных случайных величин, плотности распределения которых не являются симметричными, удобно характеризовать медианой.

Медиана случайной величины Т есть такое ее значение, которое делит площадь под кривой плотности распределения пополам.

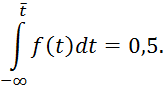
Следовательно, относительно медианы равновероятно получение большего или меньшего значения случайной величины.

Модой М₀непрерывной случайной величины Т является такое ее значение, которому соответствует наибольшее значение плотности распределения, т. е. f(M₀)=max.

Для определения теоретических значений интегральной и дифференциальной функций распределения наработок на отказ необходимо учитывать ряд особенностей нормального закона распределения.

Чаще всего, он проявляется тогда, когда случайная величина Т является результатом действия достаточно большого числа различных факторов, но все они оказывают относительно малое влияние. Нормальный закон распределения используется для описания постепенных изменений технических параметров агрегатов и систем машин, когда доля внезапных отказов мала. Этот закон распределения характерен для постепенных (износовых) отказов.

Для этого закона плотность распределения вероятности имеет вид:

 

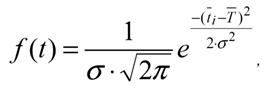где ,σ - параметры нормального распределения.

Нормальное распределение обладает рядом свойств:

- кривая распределения симметрична относительно точки t= ,через которую проходит ордината;

- кривая распределения достигает максимальной величины равной при

- ветви кривой при t→∞ асимптотически приближаются к оси абсцисс;

- при уменьшении σ кривая распределения вытягивается вверх, сжимаясь с боков, а при увеличении σ кривая распределения вытягивается вдоль оси абсцисс;

- в интервале от -σ до σ заключено приблизительно 68,3 % всей площади под кривой, от -2σ до +2σ − 95,5 % и от -3σ до +3σ − 99,7 %.

Отсюда видно, что рассеивание случайной величины с незначительной погрешностью укладывается на интервале ± 3σ.

Для упрощения вычислений введем величину . Такая замена называется нормированием:

 

                                                                                  .                                         

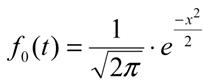Знак аргумента не имеет значения f₀(-x)=f₀(x),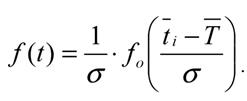

Табулированные значения функции f0(x) представлены в таблице А.1 приложения.

Вероятность безотказной работы до первого отказа вычисляется с помощью уравнения: