Рис. 5.6. Схематическое изображение потенциальных барьеров в жидкости.
Тепловое движение ее в этом состоянии сводится к колебаниям около центра равновесия с частотой
v»kT/h, (5.9)
где h - постоянная Планка, k - постоянная Больцмана, Т - температура, К. Обычно v = 1012 -1013 1/с. Как для ионов, так и для молекул в жидкости имеется ощутимая вероятность приобретения за счет теплового движения энергии, достаточной для отрыва от соседней молекулы и перемещения на расстояние, соизмеримое с размерами молекул или ионов. При этом ион остается в сфере влияния окружающих его молекул и ионов.
Необходимая для такого перемещения энергия активации Waопределяется высотой потенциального барьера между квазиустойчивыми положениями 1 и 2. При этом вероятность приобретения частицей за счет теплового движения энергии, равной или большей
Wa = 
(5.10)
Каждая жидкость в той или иной степени диссоциирована и содержит определенное количество ионов n0 в единице объема.
Степень диссоциации αД (отношение числа диссоциированных молекул n0 к общему числу молекул п в единице объема жидкости) зависит от диэлектрической проницаемости жидкости, причем полярные жидкости всегда более сильно диссоциированы. Например, для трансформаторного масла αД = 10-11 , а для касторового масла αД = 10-8.
При отсутствии внешнего электрического поля ионы и молекулы в жидкости движутся хаотически. При этом в среднем можно принять, что вдоль каждой из трех взаимно перпендикулярных осей движется n0/3 ионов, причем из положения 1 в положение 2 (также, как из положения 2 в положение 1) перемещается n0/6 ионов. Считая, что при каждом колебании ион совершает попытку перейти из квазиустойчивого положения 1 в соседнее квазиустойчивое положение 2 (или обратно), число перемещений в заданном направлении, совершаемых в единицу времени в единице объема, равно
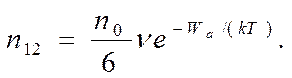(5.11)
При наложении электрического поля с напряженностью Е происходит смещение распределения потенциальной энергии. Изменение потенциальной энергии частицы с зарядом qi при перемещении ее на расстояние х за счет внешнего поля в направлении напряженности этого поля составляет
(5.12)
В этом случае изменение потенциальной энергии частицы с зарядом qi вдоль оси х иллюстрирует кривая II рис 5.6. При наложении электрического поля величина n12 становится больше n21, причем число избыточных переходов в единицу времени в единице объема в направлении электрического поля равно
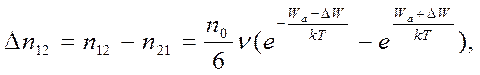(5.13)
где ΔW=qiEδ/2, δ – расстояние между двумя квазиустойчивыми положениями 1 и 2.
При малых напряженностях ΔW << kT
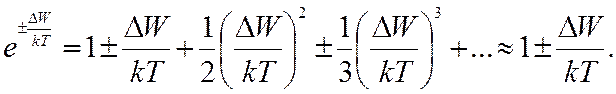(5.14)
Учитывая (5.13) и (5.14):
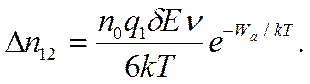(5.15)
Направленная скорость перемещения ионов на основании (5.15) равна:
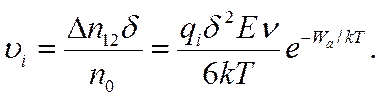(5.16)
и подвижность ионов
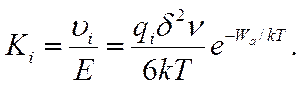(5.17)
При этом удельная объёмная проводимость:
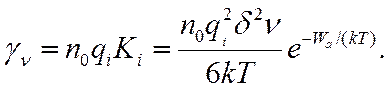(5.18)
Подвижность как положительных, так и отрицательных ионов (групп ионов) в слабых полях для минеральных масел имеет величину 10-8 м2/(с·В). В сильных полях подвижность отрицательных ионов заметно возрастает и достигает величины 10-7 м2/(с·В), подвижность положитель-ных ионов остается практически неизменной.
Формула (5.18) удельной объемной проводимости может быть также представлена в следующем виде:
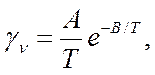(5.19)
где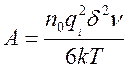 
и B=Wа/k -
константы, практически не зависящие от температуры. Так как величина А/Т по
сравнению с членом е-В/Т меняется незначительно, то
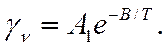(5.20)
В небольшом интервале температур зависимость γv от температуры может быть также представлена в виде:
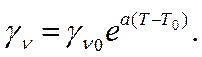(5.21)
где γv0 – проводимость при температуре Т0, а -температурный коэффициент увеличения проводимости.
Для ряда жидких диэлектриков проводимость тесно связана с вязкостью ηВ, которая зависит от температуры по формуле:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.