Пробой диэлектриков. Элементарные процессы при разряде в газе. Электрическая прочность электроизоляционных материалов. Основные виды пробоя, страница 15

,	СИ	U   f     S     d     T	(5.38)
		B  Гц   м2   м     ºС

где U – приложенное напряжение; ¦ – частота; e – относительная диэлектрическая проницаемость (считаем ее зависящей от температуры); tgd₀ – тангенс угла потерь диэлектрика при температуре окружающей среды; a – температурный коэффициент тангенса угла диэлектрических потерь; Т – температура нагретого за счет диэлектрических потерь материала

Т₀ – температура окружающей среды; S – площадь электрода; d – толщина диэлектрика.

Uпр     кВ

                    

 

U1

U∞                    

t, с

	t1

 

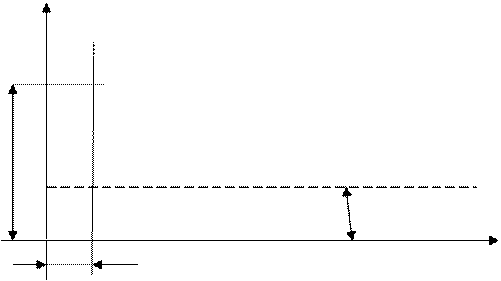
Рис. 5.16. Зависимость пробивного напряжения U_пр при электротепловом пробое от времени приложения напряжения.

Мощность, выделяемая в объеме диэлектрика, пропорциональна тангенсу угла диэлектрических потерь. Мощность, отводимая от диэлектрика, пропорциональна площади теплоотвода и  разности температур диэлектрика и среды. Условию теплового равновесия диэлектрика с окружающей средой соответствует равенство мощностей. С повышением температуры диэлектрика, начиная с некоторой критической (Ткр), может возникнуть такая ситуация, когда тепловыделение в объеме будет превосходить потери тепла за счет теплоотвода. Диэлектрик лавинообразно разогревается, происходят теплохимические превращения и разрушение диэлектрика.

Условия возникновения теплового пробоя проиллюстрируем на неполярном электроизоляционном материале, в котором проявляются только диэлектрические потери на электропроводность. Количество электрической энергии, которое при этом превращается в диэлектрике в теплоту, выражается формулой (4.1, тема 4)

Диэлектрические потери повышаются с ростом температуры экспоненциально. Характер изменения потерь в зависимости от температуры показан на рис. 5.17 (кривые 1 - 3).

СИ РТ Т s S Дж К м2

Количество теплоты, которую электроизоляционный материал способен отвести за единицу времени через поверхность в окружающую среду, выражается формулой Ньютона

PT=2σS(T-T0) ,                                                                                                                   (5.39)

где R_т – количество теплоты, отведенной за единицу времени в окружающую среду; σ – коэффициент теплоотдачи; S – поверхность электроизоляционного материала; T₀ – температура окружающей среды; T – температура электроизоляционного материала.

Ра при U₂                  Ра при U₃

 

Ра при  U₁

                          Р                                   1        2  3            4

 

Рт

 

Т₀   Т₁             Т₃                 Т₂        Т

Рис. 5.17. Выделение и отвод теплоты в электроизоляционном материале: кривая 1-тепловыделение (Ра) при U₁;  кривая 2-(Ра) при U₂;  кривая 3-(Ра) при U₃;  кривая 4 – отводимая теплота; U₁>U₂>U₃; T₃=Tкр

В отличие от потерь количество отведенной теплоты за единицу времени (мощность теплового потока) повышается с температурой линейно (прямая 4 на рис. 5.17).

При таком рабочем режиме  электроизоляционного материала, при котором его потери соответствуют кривой 1, постоянно возникает теплоты больше, чем электроизоляционный материал может отвести (возникает тепловой разбаланс), поэтому его температура непрерывно повышается, пока не наступит тепловая деструкция (расплавление, обугливание и т.п.). Тепловыделение Ра при U₂.

При режиме, соответствующем кривой 2, электроизоляционный материал после подключения к источнику начинает разогреваться и его температура остановится на уровне Т₃, где количество возникшей теплоты соответствует количеству теплоты, которую электроизоляционный материал может отвести в окружающую среду. Это, однако, температура неустойчивого равновесия, так как уже при небольшом перенапряжении в сети равновесие полностью нарушается. После этого температура электроизоляционного материала будет непрерывно повышаться вплоть до тепловой деструкции. Тепловыделение Р_а при U₂.