Самым выгодным является режим, соответствующий кривой 3. После подачи напряжения температура электроизоляционного материала вследствие потерь увеличивается до уровня Т1, где наступает устойчивое равновесие. Если по какой-либо причине увеличатся потери, электроизоляционный материал несколько нагреется, но затем снова охладится, так как количество теплоты, которую он способен отвести в окружающую среду, превышает количество образовавшейся теплоты. И только при дальнейшем увеличении Т потери вызовут разогрев до уровня Т2, возникнет неустойчивое равновесие и при дальнейшем увеличении потерь необратимо наступит тепловая деструкция электроизоляционного материала. Тепловыделение Ра равно теплопередачи Рт.
Необходимо учесть, что повышение температуры электроизоляционного материала имеет следствием повышение его удельной электрической проводимости, а это снова имеет следствием дальнейшее повышение температуры и т.д.
Напряжение U1, при котором возникает неустойчивый граничный режим, может быть принято за напряжение теплового пробоя Uпр и определяется из равенства:
|
|
Условие (5.9) справедливо для граничного режима, а условие (5.40) выполняется для всех случаев устойчивой работы (устойчивого равновесия) диэлектрика под напряжением.
Исходя из 5.38 … 5.40 получаем
|
|
(5.41) |
|
|
(5.42) |
Разделив выражение (5.41.) на (5.42.), получим
|
|
(5.43) |
Подставляя (5.38.) в (5.39.) и решая его относительно U получим
|
|
(5.44) |
где К –
числовой коэффициент, равный ![]() , если все величины
имеют размерности, выраженные в единицах Си.
, если все величины
имеют размерности, выраженные в единицах Си.
Как видно, электрическая прочность в случае теплового пробоя зависит не только от свойств материала (относительной диэлектрической проницаемости, тангенса угла потерь, коэффициента теплопередачи), но и от температуры, частоты, а также от условий охлаждения (теплопроводности окружающей среды, площади поверхности электроизоляционного материала, его толщены и т.п.).
Для возникновения теплового пробоя необходимо определенное время, пока температура повысится до опасного уровня, поэтому время от приложения электрического поля до теплового пробоя существенно больше, чем при электрическом пробое. Иногда оно имеет порядок нескольких минут и даже часов.
Рассмотрение механизма теплового пробоя выявляет факторы (возникает период температуры по слоям диэлектрика, что ведет к искажению электрического поля и повышенным градиентам напряжения по слоям, влияет теплопроводность материала электродов) приводящие к снижению пробивного напряжения определяемого по формуле (5.43).
В.А. Фоком и Н.Н. Семеновым, с учетом перечисленных факторов, при постоянном и переменном напряжениях для одномерного потока теплоты через электроды получена формула для определения пробивного напряжения в виде
|
|
СИ |
γ f U |
(5.45) |
|
Вт/м·к Гц В |
где ![]() –
коэффициент теплопроводности диэлектрика, j(с)
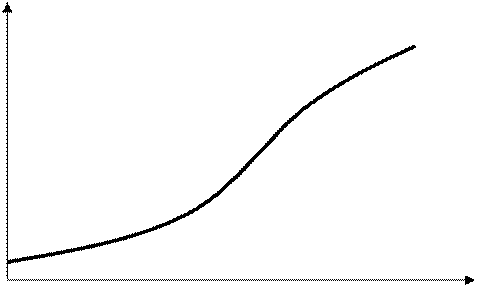
– функция, значения которой для плоских образцов находят из графика j(с) = ¦(с)
(рис. 5.18), с – аргумент, определяемый из выражения:
–
коэффициент теплопроводности диэлектрика, j(с)
– функция, значения которой для плоских образцов находят из графика j(с) = ¦(с)
(рис. 5.18), с – аргумент, определяемый из выражения:
|
|
СИ |
σ |
(5.46) |
|
Вт/м2·к м |
где ![]() –
коэффициент теплопроводности материала электродов; s – коэффициент теплопередачи в электроды;
–
коэффициент теплопроводности материала электродов; s – коэффициент теплопередачи в электроды; ![]() – толщина электрода.
– толщина электрода.
При неограниченном возрастании С в функции j(с) равно 0,663 и тогда
|
|
(5.47) |
То есть пробивное
напряжение при тепловом пробое не может быть больше ![]() максимального.
максимального.
 φ
φ
0,6
0.5
0.4
0.3
0.2
0.1
0 0.02 0.1 1 10 с
Рис 5.18 Зависимость φ(с), используемая при расчете напряжения теплового пробоя по В. А. Фоку и Н. Н. Семенову
5.6.3. Ионизационный пробой
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.