Из выражения (1.7) может быть получена формула для определения разброса собственной емкости катушки в зависимости от разброса ее геометрических параметров и свойств материалов:
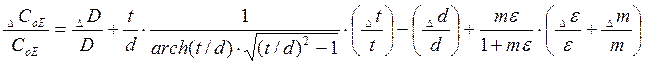 (1.8)
(1.8)
Из уравнения (1.8)
видно, что на разброс ![]() оказывают влияние погрешности
размеров диаметра катушки
оказывают влияние погрешности
размеров диаметра катушки ![]() и разброс связи провода
намотки с каркасом, характеризующийся величиной
и разброс связи провода
намотки с каркасом, характеризующийся величиной ![]() .
.
Кроме того, разброс ![]() обусловлен
разбросом диэлектрической проницаемости
материала каркаса, а также допуском на диаметр провода, причем при равенстве
шага намотки диаметру провода, разброс
возрастает при прочих равных условиях.
обусловлен
разбросом диэлектрической проницаемости
материала каркаса, а также допуском на диаметр провода, причем при равенстве
шага намотки диаметру провода, разброс
возрастает при прочих равных условиях.
Добротность Q катушки количественно равна величине отношения ее реактивного сопротивления к сопротивлению потерь
![]() :
:
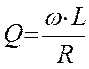 , (1.9)
, (1.9)
где ![]() - частота электрических
колебаний в цепи,
- частота электрических
колебаний в цепи, ![]() ;
;
![]() ;
;
![]() - активное сопротивление
провода намотки переменному току, Ом;
- активное сопротивление
провода намотки переменному току, Ом;
![]() - сопротивление,
обусловленное диэлектрическими потерями в каркасе, Ом;
- сопротивление,
обусловленное диэлектрическими потерями в каркасе, Ом;
![]() -
сопротивление, вносимое
сердечником, Ом;
-
сопротивление, вносимое
сердечником, Ом;
![]() - сопротивление, вносимое
экраном, Ом.
- сопротивление, вносимое
экраном, Ом.
Добротность характеризует резонансные свойства и КПД колебательного контура. Современные катушки индуктивности приемлемых размеров и средней стоимости имеют добротность порядка 50-300.
При протекании переменного ток через катушку индуктивности активное сопротивление провода ее намотки значительно выше сопротивления постоянному току вследствие поверхностного эффекта и эффекта близости, которые увеличивают плотность тока во внутренних областях витков и тем самым уменьшают действующее сечение проводника.
Поверхностный эффект проявляется в увеличении активного сопротивления проводника с ростом частоты переменного тока, так как под действием переменного магнитного поля в проводе происходит перераспределение плотности тока (увеличение в наружных слоях и уменьшение во внутренних).
Уменьшение составляющей ![]() ,
вызванное проявлением поверхностного
аффекта, достигается путем увеличения диаметра провода, нанесения покрытий, обладающих низким
сопротивлением (чаще всего серебрение),
и уменьшения шероховатости поверхности.
,
вызванное проявлением поверхностного
аффекта, достигается путем увеличения диаметра провода, нанесения покрытий, обладающих низким
сопротивлением (чаще всего серебрение),
и уменьшения шероховатости поверхности.
Эффект близости проявляется при изгибе проводника. Магнитное поле становится несимметричным относительно сечения провода, смещает ток внутрь витка, увеличивая активное сопротивление катушки. Проявление этого эффекта тем сильнее, чем, больше диаметр провода и меньше диаметр катушки.
Исходя из характера изменения составляющих, можно установить, что при вполне определенном диаметре провода (оптимальном) сопротивление будет иметь минимальное значение.
Для однослойных катушек с шагом оптимальный диаметр провода с достаточной степенью точности вычисляют по формуле:
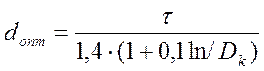 ,
(1.10)
,
(1.10)
где ![]() - шаг
намотки, мм, при этом
- шаг
намотки, мм, при этом
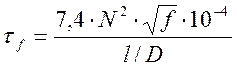 ,
,
где ![]()
![]() - частота, МГц.
- частота, МГц.
Сопротивление ![]() , обусловленное потерями
в диэлектрике каркаса, может быть
рассчитано по формуле:
, обусловленное потерями
в диэлектрике каркаса, может быть
рассчитано по формуле:
![]() ; (1.11)
; (1.11)
где ![]() - в пФ;
- в пФ;
![]() - угол потерь в диэлектрике каркаса;
- угол потерь в диэлектрике каркаса;
![]() - в мкГн;
- в мкГн;
![]() - в МГц.
- в МГц.
Практически диэлектрические потери проявляются лишь в катушках большого диаметра, имеющих большую собственную емкость, и каркасы, выполненные из низкокачественного диэлектрика (картона, бакелита, а на УКВ - пирофелита, радиофарфора).
В катушках малого размера с каркасами из ультрафарфора или полистирола диэлектрические потери ничтожно малы.
Катушки с незамкнутыми магнитными сердечниками обладают
значительным внешним полем, которое обусловливает связь между различными контурами. Чаще всего такая связь паразитная. Для ее уменьшения применяют экранирование.
Активное сопротивление, вносимое экраном в катушку индуктивности, может быть определено из выражения:
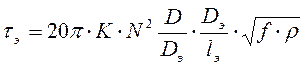 ,
(1.12)
,
(1.12)
где 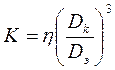 - коэффициент связи между катушкой и
экраном;
- коэффициент связи между катушкой и
экраном;
![]() - коэффициент, зависящий от
- коэффициент, зависящий от ![]() ;
;
![]() - диаметр экрана, мм;
- диаметр экрана, мм;
![]() - высота экрана, мм;
- высота экрана, мм;
![]() - в МГц;
- в МГц;
![]() - удельное сопротивление материала экрана,
- удельное сопротивление материала экрана, ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.