3) От каких конструктивных параметров зависит собственная емкость катушки индуктивности?
4) Как влияют сердечники на электрические параметры катушек индуктивности?
5) Как влияют экраны на электрические параметры катушек индуктивности?
Для подготовки к данной лабораторной работе рекомендуется использовать следующую литературу: [2, с. 170-238; I, с. 202-312; 3, с. 135-195].
Необходимо помнить, что
катушка индуктивности - основной элемент колебательных контуров, фильтров к линий
задержки. В данной работе изучают следующие параметры катушек: индуктивность (L), добротность (Q), собственную емкость (![]() ).
).
Индуктивность определяется
как отношение потокосцепления ![]() к току
к току ![]() . Необходимо определить индуктивность
отрезка проводника круглого сечения - простейшей конструкции
токопровода:
. Необходимо определить индуктивность
отрезка проводника круглого сечения - простейшей конструкции
токопровода:
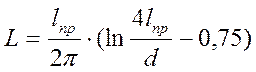 ,
(1.1)
,
(1.1)
где ![]() - длина;
- длина;
![]() - диаметр проводника.
- диаметр проводника.
При сворачивании проводника
длиной ![]() в кольцо диаметром
в кольцо диаметром ![]() индуктивность уменьшается. Однако
индуктивность кольца является наибольшей по сравнению с индуктивностью витка
другой конфигурации, поскольку круглый виток охватывает наибольшую площадь,
обеспечивал наибольшее потокосцепление.
индуктивность уменьшается. Однако
индуктивность кольца является наибольшей по сравнению с индуктивностью витка
другой конфигурации, поскольку круглый виток охватывает наибольшую площадь,
обеспечивал наибольшее потокосцепление.
Индуктивность круглого
плоского витка диаметром ![]() из провода круглого
сечения диаметром
из провода круглого
сечения диаметром ![]() следует определять по формуле:
следует определять по формуле:
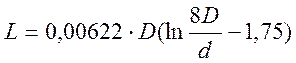 .
(1.2)
.
(1.2)
При сворачивании
проводника длиной ![]() в несколько витков N одинакового
диаметра образуется катушка, индуктивность которой может быть определена как
сумма индуктивностей витков и взаимоиндук-тивностей между ними:
в несколько витков N одинакового
диаметра образуется катушка, индуктивность которой может быть определена как
сумма индуктивностей витков и взаимоиндук-тивностей между ними:
![]() , (1.3)
, (1.3)
где ![]() - индуктивность витка;
- индуктивность витка;
![]() -
взаимоиндуктивность между
-
взаимоиндуктивность между ![]() и
и
![]() - витками;
- витками;
![]() ,
(1.4)
,
(1.4)
где ![]() - диаметр каркаса (витка), см;
- диаметр каркаса (витка), см;
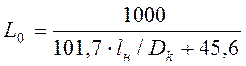 -
коэффициент формы;
-
коэффициент формы;
![]() -
длина намотки, см.
-
длина намотки, см.
Индуктивность однослойных катушек не превышает 200-250 мкГн, причем целесообразность перехода на многослойную намотку определяется диаметром катушки: чем больше диаметр катушки, тем при большем требуемом значении индуктивности следует переходить на многослойную намотку.
При изготовлении катушки,
рассчитанной согласно формуле (1.4), разброс индуктивности ![]() следует
определять по формуле:
следует
определять по формуле:
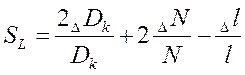 ,
(1.5)
,
(1.5)
из которой следует, что наибольшее влияние на разброс индуктивности оказывает неточность изготовления диаметра каркаса (витка). Поэтому допуск на его размер должен бить достаточно жестким.
Собственная емкость катушки обычно
рассматривается как некоторая емкость ![]() , подключенная
к выводам катушки. Величина собственной емкости определяется типом намотки и
размерами катушки. При этом надо иметь в
виду, что наименьшей собственной емкостью
(1-2 пФ) обладают однослойные катушки, намотанные с шагом. Величина
, подключенная
к выводам катушки. Величина собственной емкости определяется типом намотки и
размерами катушки. При этом надо иметь в
виду, что наименьшей собственной емкостью
(1-2 пФ) обладают однослойные катушки, намотанные с шагом. Величина ![]() у однослойной катушки индуктивности
определяется диаметром намотки
у однослойной катушки индуктивности
определяется диаметром намотки ![]() , отношением шага
намотки
, отношением шага
намотки ![]() к диаметру провода
к диаметру провода ![]() ,
длиной намотки
,
длиной намотки ![]() , изоляцией провода, материалом
каркаса и его формой. Для расчета величины собственной емкости однослойной
катушки, намотанной без каркаса или на гладком цилиндрическом каркасе из
материала с невысокой диэлектрической проницаемостью
, изоляцией провода, материалом
каркаса и его формой. Для расчета величины собственной емкости однослойной
катушки, намотанной без каркаса или на гладком цилиндрическом каркасе из
материала с невысокой диэлектрической проницаемостью ![]() ,
можно использовать выражение:
,
можно использовать выражение:
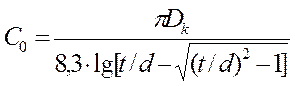 ,
(1.6)
,
(1.6)
где ![]() даны в
см.
даны в
см.
Зная диэлектрическую
проницаемость материала каркаса, собственную емкость ![]() однослойной
катушки можно определить по формуле
однослойной
катушки можно определить по формуле
![]() ,
(1.7)
,
(1.7)
где ![]() - коэффициент,
зависящий от типа намотки.
- коэффициент,
зависящий от типа намотки.
Собственную емкость
однослойной катушки, величина которой достигает единиц пикофарад, можно разделить на две составляющие: "через воздух" ![]() и "через
диэлектрик"
и "через
диэлектрик" ![]() .
.
Обычно на разброс величины собственной емкости не обращают внимания, однако, когда к катушкам предъявляют требования высокой устойчивости, необходимо, по возможности, исключить разброс всех основных параметров катушки, в том числе и ее собственной емкости, та последняя увеличивает действующую индуктивность и снижает стабильность катушки.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.