Необходимо знать, что искажение формы обусловливают сложные переходные процессы, так как трансформатор имеет индуктивности и емкости. Искажение трансформируемого импульса проявляется в увеличении времени его нарастания, спаде заднего фронта, снижении вершины и возникновении затухающих колебаний (рис. 7.1 а, б, в соответственно).
Студент должен знать, что любое периодическое несинусоидальное колебание можно разложить в бесконечный тригонометрический ряд, состоящий из постоянной и синусоидальных составляющих различной частоты, амплитуды и фазы, совокупность которых составляет частотный спектр. При этом получают тригонометрический ряд (ряд Фурье):
|
|
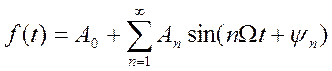 ,
(7.1)
,
(7.1)
где ![]() - несинусоидальная периодическая функция с
периодом
- несинусоидальная периодическая функция с
периодом
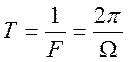 ;
;
![]() - первая гармоника с частотой,
равной частоте функции
- первая гармоника с частотой,
равной частоте функции ![]() ;
;
![]() - вторая гармоника с удвоенной
частотой и т.д.
- вторая гармоника с удвоенной
частотой и т.д.
На рис. 7.2.а приведен частотный спектр одиночного прямоугольного импульса со сплошным спектром. При значительном числе импульсов в серии спектр можно считать дискретным (рис.7.2.б).
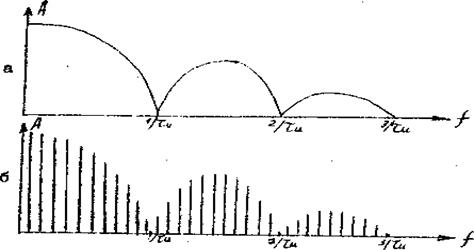
Рис. 7.2
Из графика частотного
спектра прямоугольных импульсов видно, что после каждого нуля максимальные значения
огибающей спектра падают. Поэтому наибольшее значение имеют гармоники, лежащие
до первого нуля, т.е. до частоты 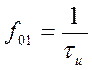 . Отсутствие
высших гармоник в составе импульсов приводит к увеличению
длительности фронта. Полосу пропускания радиоэлектронных устройств следует
принимать
. Отсутствие
высших гармоник в составе импульсов приводит к увеличению
длительности фронта. Полосу пропускания радиоэлектронных устройств следует
принимать
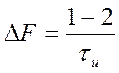 .
(7.2)
.
(7.2)
В устройствах, где необходимо получить большую крутизну (малую длительность) фронта, в радиолокационных станциях полосу пропускания берут шире:
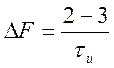 .
(7.3)
.
(7.3)
Следует знать, что широкая полоса пропускания, достигающая десятков
мегагерц, является характерной особенностью импульсных устройств. Так, при
трансформации прямоугольных импульсов длительностью ![]() , трансформатор должен
иметь полосу пропускания равной 1 МГц.
, трансформатор должен
иметь полосу пропускания равной 1 МГц.
При изучении данного
вопроса необходимо уяснить, от каких параметров зависит полоса пропускания
импульсного трансформатора и какими конструктивными мерами можно ее расширить,
в области низких и высоких частот. Однако при расчетах импульсных трансформаторов
удобнее связывать параметры трансформатора непосредственно с искажениями формы
импульса, поскольку конструктору, как правело, заданы
длительность трансформируемого импульса ![]() , амплитуда
импульса на входе
, амплитуда
импульса на входе ![]() , амплитуда импульса на выходе
трансформатора
, амплитуда импульса на выходе
трансформатора ![]() , требуемая длительность фронта
импульса
, требуемая длительность фронта
импульса ![]() , значение спада плоской части импульса
, значение спада плоской части импульса 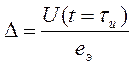 . Последнее зависит от величины индуктивности первичной обмотки и, следовательно,
определяет амплитудно-частотную характеристику трансформатора в области,
низких частот. Связь величины индуктивности
. Последнее зависит от величины индуктивности первичной обмотки и, следовательно,
определяет амплитудно-частотную характеристику трансформатора в области,
низких частот. Связь величины индуктивности ![]() со
значением спада плоской части импульса
определяется выражением
со
значением спада плоской части импульса
определяется выражением
![]() ,
(7.4)
,
(7.4)
где
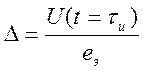 ;
(7.5)
;
(7.5)
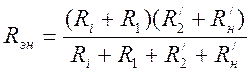 ; (7.6)
; (7.6)
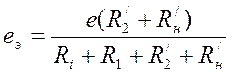 .
(7.7)
.
(7.7)
Обычно в качестве характеристики длительности фронта
импульса берут время, в течении которого напряжение на загрузке ![]() изменяется от уровня 0.1 до уровня 0.9.
При этом длительность фронта импульса связана с индуктивностью рассеяния
следующим соотношением:
изменяется от уровня 0.1 до уровня 0.9.
При этом длительность фронта импульса связана с индуктивностью рассеяния
следующим соотношением:
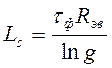 ,
(7.8)
,
(7.8)
где ![]() .
.
Таким образом, чем меньше требуемая длительность фронта импульса, тем меньше допустимая индуктивность рассеяния.
При жестких требованиях к
форме импульса, т.е. при ![]() и
и ![]() , конструктивное выполнение импульсного трансформатора вызывает много трудностей из-за
противоречивости требований увеличения
, конструктивное выполнение импульсного трансформатора вызывает много трудностей из-за
противоречивости требований увеличения ![]() и
уменьшения
и
уменьшения ![]() и
и ![]() .
.
Наличие паразитной емкости
трансформатора вызывает дополнительные искажения формы импульса ![]() и
и
![]() образуют контур ударного возбуждения, в котором
возникают затухающие колебания (см.
рис. 7.1,в). Наличие затухающих колебаний нежелательно также и потому, что при нарастании переднего
фронта импульса напряжение на
вторичной обмотке может достигать значения 2
образуют контур ударного возбуждения, в котором
возникают затухающие колебания (см.
рис. 7.1,в). Наличие затухающих колебаний нежелательно также и потому, что при нарастании переднего
фронта импульса напряжение на
вторичной обмотке может достигать значения 2 ![]() , о
результате чего возможны пробои в трансформаторе.
, о
результате чего возможны пробои в трансформаторе.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.