Методические указания по лабораторным работам “Устройства функциональной электроники и электрорадиоэлементы”, “Электроэлементы ЭВА”, страница 12

Полученные значения сравнить с табличными. Для принятого в эксперименте уровня значимости  = 0,05 и числа степеней сво­боды   f  =n-1 = 3-1 = 2 табличное значение   (или 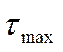 ) равно 1,69.

Если полученные значения 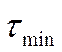   или     окажутся меньше табличных, то гипотеза о принадлежности всех откликов данной со­вокупности и случайном  отличии данного члена от остальных подт­верждается (нет грубых ошибок).

В противном случае резко выделяющейся член выборки дожжен быть исключен из дальнейшей обработки (или проведено повторное намерение данного значения ).

5.5.5. Определить построчные средние значения    и оценки поc- трочных дисперсий    по формулам:

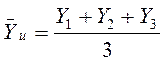     ;                                                         (5.10)

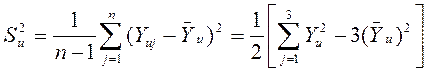   .                    (5.11)

5.5.6. Проверить однородность  построчных  дисперсий  по крите­рию (статистике)  Корена     по формуле

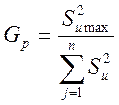                   ,                                                   (5.12)

где   - наибольшая из всех N построчных дисперсий.
При этом необходимо иметь в виду, что здесь  и . По уровню значимости = 0,05 и значением   и  из распределения Корена находят табличное значение .

Для значений   и N  в данном эксперименте табличное зна­чение статистики Корена    = 0,41. Если окажется,  что , то оценка     считается однородной. В  противном  случае построч­ные дисперсии не однородны и не выполняется основное допущение регрессивного анализа равноточности измерений отклика во всех строках плана, что делает бессмысленной дальнейшую обработку ре­зультатов  эксперимента  я требует повторных измерений   .

5.5.7. Определить дисперсии воспроизводимости     no фор­муле

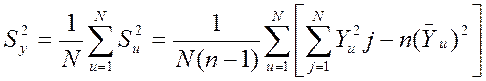     .                   (5.13)

В этом случае со статистикой  связано   число степеней свободы.

        5.5.8. Для принятого в данной работе уравнения регрессии

                                                       (5.14)

 определить  - коэффициенты в скалярной форме по формуле

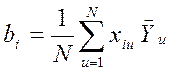            ,                                           (5.15)

 где     для  ПФЭ  (в данной работе  N=4).

5.5.9. Проверить статистическую значимость этих коэффициентов по критерию Стьюдента

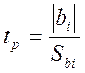                 ,                                                                     (5.16) где 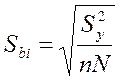   - оценка среднеквадратичного отклонения коэффи­циента ,  а значение    определено ранее no (5.I3). С ве­личиной

 число степеней свободы связано соотношением

         Для    и  значение   = 2,306.

Если окажется, что , то коэффициент  следует положить равным 0 , в противном случае соответствующий член остается в уравнении регрессии.

5.5.10. Проверить адекватность модели с использованием крите­рия Фишера путем нахождения дисперсии адекватности по формуле

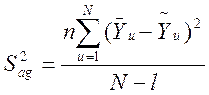        ,                                                    (5.17)

 где 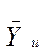   - среднее значение отклика в n- точке плана;

   - предсказанное значение отклика в той же точке плана (определяется по (5.14) путем подстановки в уравнение значений X);

     - общее число значимых коэффициентов в уравнении рег­рессии (<N);

            n - число параллельных опытов во всех точках плана (n=3).

        После этого определяют расчетное значение

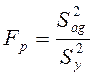,                                                           (5.18)

с которым связано число степеней свобода дисперсии адекватности             - число степеней свободы дисперсии
воспроизводимости.                        

По табл. 5.3 находят табличное значение    с учетом значе­ний

,  и .

                 Таблица   5.3

                                     Значения