Нестационарный теплообмен. Нестационарная теплопроводность. Нестационарный процесс конвективного теплообмена

ЛЕКЦИЯ 20 Нестационарный теплообмен

20.1. Общие сведения

Нестационарными тепловыми процессами называют процессы теплообмена, протекающие в изменяющемся во времени температурном поле. Особенностью этих процессов является непрерывное изменение теплосодержания тел и связанное с этим их нагревание или охлаждение. Чаще всего нестационарный теплообмен наблюдается в периодически действующих аппаратах (нагревание или охлаждение твердых тел, неподвижных масс жидкостей, кристаллизация из растворов и расплавов, процессы в химических реакторах и т.д.). В непрерывно действующих теплообменных аппаратах нестационарный перенос тепла возникает лишь в периоды пуска, остановки или изменения режима их работы.

При расчете нестационарных процессов теплообмена определяют либо время, необходимое для нагревания или охлаждения до заданной температуры, либо конечную температуру, которая достигается за то же время, а также количество тепла, переданное телу или отнятое от него. В случае жидких или газообразных веществ определяют лишь зависимость их средней температуры от времени, так как температура жидкости и газа всегда выравнивается за счет конвекции, сопутствующей теплопроводности.

20.2. Нестационарная теплопроводность

Нестационарные процессы теплопроводности протекают в случае нагревания или охлаждения твердых тел при их непосредственном соприкосновении с горячими или холодными потоками жидкостей или газов.

На рис. 20.1 показан характер изменения температур на поверхности t_пов и в глубине тела t_гл, внесенного в среду с более высокой температурой t_ж.

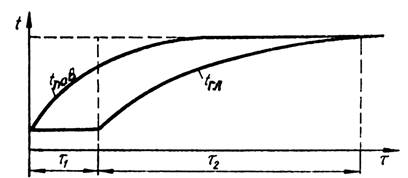
Рисунок 20.1 – Характер изменения температуры
тела во времени

Любой процесс нагревания или охлаждения тела можно разделить на три режима. Первый из них охватывает начало процесса и характеризуется постепенным изменением температуры в глубь тела (участок τ₁). При этом скорость изменения температуры в отдельных точках различна, а температурное поле зависит от начального распределения температур в теле. Этот режим носит название неупорядоченного. В дальнейшем влияние начального распределения температур в теле исчезает, и относительная скорость изменения температуры в каждой точке тела становится постоянной величиной, зависящей от формы и размеров тела, его теплофизических свойств, условий теплообмена на поверхности тела. Такой упорядоченный режим нагрева назван регулярным (участок τ₂). По истечении длительного времени (теоретически по истечении бесконечно большого времени) наступает третий, стационарный режим, характерной особенностью которого является постоянство распределения температур во времени, в каждой точке тела . Если температура во всех точках тела одинакова и равна температуре окружающей среды, то наступает режим теплового равновесия.

Решение задачи нестационарной теплопроводности заключается в определении зависимости изменения температуры во времени для любой точки тела t и количества подведенной или отведенной теплоты. Это может быть осуществлено аналитическим путем в результате решения дифференциального уравнения теплопроводности при Q = 0 совместно с условиями однозначности.

Для технических целей в большинстве случаев ограничиваются рассмотрением течения процесса лишь в одном каком-либо направлении – направлении х, например. В этом случае

                                         .

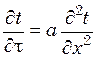Краевыми условиями для аналитического решения дифференциального уравнения теплопроводности являются:

а) начальное распределение температуры в теле

б) действие на поверхность тела окружающей среды.

Последнее условие может быть задано тремя способами:

1) распределением температуры на поверхности тела t_пов в любой момент времени τ – граничное условие 1-го рода;

2) распределением плотности теплового потока по поверхности тела q_пов во времени – граничное условие 2-го рода;

3) распределением температуры окружающей среды t_ж и коэффициентом теплоотдачи  от поверхности тела к этой среде: 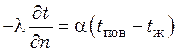 – граничные условия 3-го рода.

Тогда дифференциальные уравнения теплопроводности для тел различной геометрической формы принимают следующий вид.

Для плоской неограниченной стенки толщиной 2δ, омываемой жидкостью с температурой t_ж ,

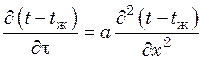                                .                               (20.1)

Краевые условия при этом:

                            ; ;

                                  ; ,

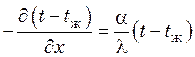где t₀ – температура в начальный момент времени, равная температуре поверхности стенки.

Для сплошного цилиндра неограниченной длины

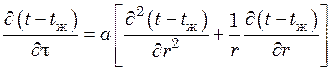                     .                    (20.2)

Краевые условия:

                            ; ;

                                  ; ,

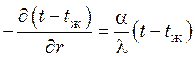(R – радиус сечения цилиндра).

Для сплошного шара с радиусом R

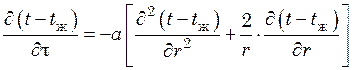                    .                  (20.3)

Краевые условия:

                           ; ;

                                  ; .

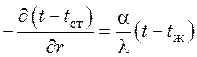Решение уравнений (20.1) – (20.3) ввиду их сложности приводятся в специальной литературе.

Предложены приближенные методы расчета, в которых пренебрегают наличием начального, неупорядоченного режима, характеризуемого неравномерным изменением температуры тела, и задачу решают относительно регулярного теплового режима. Для этого режима влияние начального распределения температуры несущественно и процесс определяется условиями теплообмена на границе твердое тело–жидкость (газ), физическими свойствами, геометрической формой и размерами тела. Для него характерна линейная зависимость

                     или .                  (20.4)