Нестационарный теплообмен. Нестационарная теплопроводность. Нестационарный процесс конвективного теплообмена, страница 2

Величина m в уравнении (20.4) является положительным числом, сохраняющим одно и то же значение для любой точки тела. Это число характеризует собой скорость охлаждения тела и называется темпом охлаждения; оно полностью определяется формой и размерами тела, значением тепловых параметров (a, l, r), интенсивностью теплообмена с окружающей средой и не зависит от начальных условий. Для ее определения достаточно измерить температуры тела t₁ и t₂ в произвольной точке тела в два определенных момента времени τ₁ и τ₂:

                       .

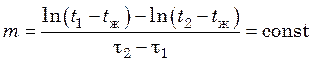В соответствии с теорией регулярного режима, разработанной Г.М. Кондратьевым, темп охлаждения m

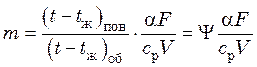                            ,                          (20.5)

где – средний перепад температур по поверхности; – средний перепад температур по объему тела; F и V – поверхность и объем тела; с_р – удельная теплоемкость тела; Y – безразмерный коэффициент пропорциональности, называемый коэффициентом неравномерности распределения температуры в теле и зависящий для данного тела от условий теплообмена между его поверхностью и окружающей средой, т.е. от критерия Био (Bi = al/l_ст); l – характерный линейный размер тел;  – коэффициент теплопроводности стенки.

При   распределение температуры в теле будет зависеть лишь от его размеров и физических свойств, поэтому  и . При   благодаря большой интенсивности внешнего теплообмена температура на поверхности стремится к температуре окружающей среды t_ж,  и . В этом случае между темпом охлаждения  и температуропроводностью тела а существует следующая зависимость:

                                          .                                         (20.6)

Коэффициент С зависит только от геометрической формы и размеров тела:

– для плоской неограниченной стенки толщиной 2δ ;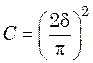

– для шара радиусом R ;

– для цилиндра радиуса R и длиной l ;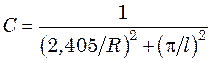

– для параллелепипеда со сторонами b₁, b₂ и b₃

                           .

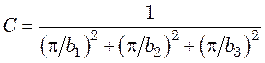По экспериментально найденным температурам t₁ и t₂ в произвольной точке тела определяют коэффициент его температуропроводности а, затем, рассчитав по уравнению (20.5) величину m, находят коэффициент теплоотдачи и скорость нагревания или охлаждения тела.

При решении ряда практических задач по нагреванию и охлаждению тел аналитический расчет можно также упростить, приняв, что перенос тепла осуществляется во времени и в пространстве не непрерывно, а скачкообразно (метод конечных разностей).

В инженерной практике наиболее часто пользуются графоаналитическим методом расчета, основанном на замене переменных, влияющих на изменение температуры тела в пространстве и во времени, безразмерными комплексами и симплексами подобия:

критерий Био                    ;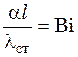

критерий Фурье

                                           ;

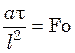симплекс геометрического подобия

                                               .

Безразмерная температура в любой точке тела  (t₀ – температура, принятая за масштаб температур) может быть выражена обобщенной зависимостью

                                   .                                  (20.7)

Эта функция постоянна для всех подобных процессов нестационарной теплопроводности.

Выражения, полученные в результате интегрирования уравнений теплопроводности для тел простой геометрической формы (плоская стенка, цилиндр, шар), представляют в виде графической зависимости безразмерных температур  на поверхности тела и в средней его плоскости  от критериев Bi и Fо. Безразмерные температуры в этом случае:

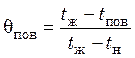                           и   ,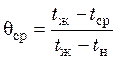

где t_ж – температура среды, принимаемая постоянной; t_пов и t_ср – температура, достигаемая за время τ соответственно на поверхности и в среднем сечении тела; t_н – начальная температура тела.