Нестационарный теплообмен. Нестационарная теплопроводность. Нестационарный процесс конвективного теплообмена, страница 3

В качестве примера на рис. 20.2 приведены зависимости  и  для плоской пограничной стенки.

Расчет по таким графикам производится следующим образом. По известным значениям λ_ст, с_р, ρ находят величину коэффициента температуропроводности  и рассчитывают критерий Фурье. Затем рассчитывают значение критерия Био, принимая за определяющий размер толщину стенки δ. При этом величина коэффициента теплоотдачи α должна быть задана или рассчитана (при расчете α задаются температурой поверхности тела, которую потом проверяют, т.е. α находят методом последовательных приближений).

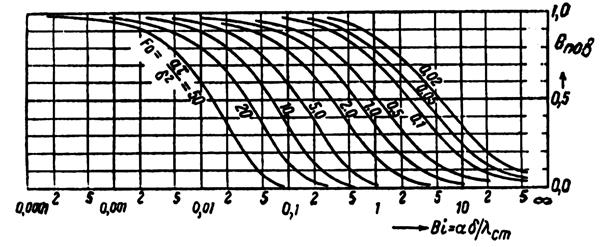
а

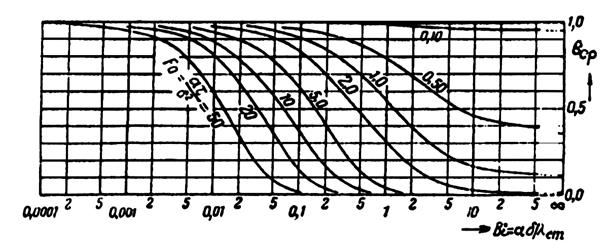
б

Рисунок 20.2 – Зависимости θ_пов и θ_ср от Вi и Fо для плоской неограниченной стенки:
а – ; б –

По пересечению перпендикуляра, проведенного из точки на оси абсцисс (рис. 20.2), соответствующей величине Вi и кривой, отвечающей значению Fо, определяют температуры θ_пов и θ_ср. По этим температурам находят температуры на поверхности t_пов и в среднем сечении стенки t_ср.

Результаты интегрирования уравнения теплопроводности можно представить также в виде зависимости

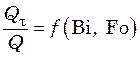                                     ,                                    (20.8)

где Q_τ – количество тепла, переданное за время τ; Q – полное количество тепла, переданное телу до наступления равновесия (до полного нагревания или охлаждения).

Расчет  производят по соотношениям:

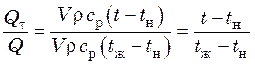.  (20.9)

В уравнении (20.9) V – объем тела; t – средняя по объему тела температура, достигнутая за время нагрева (эта температура задается или принимается).

На рис. 20.3 представлена зависимость  от критериев Био и Фурье для плоской неограниченной стенки.

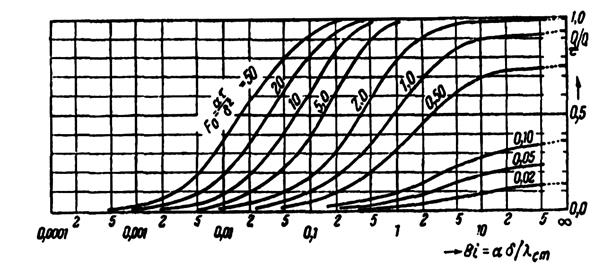
Рисунок 20.3 – Зависимость  от Bi и Fо для плоской неограниченной стенки

Для определения времени нагрева стенки до температуры t необходимо из точки на оси абсцисс (рис. 20.3), соответствующей данному значению Bi, восстановить перпендикуляр до пересечения с ординатой, отвечающей значению отношения . Точка пересечения определит величину , по которой определяется искомое время нагрева τ.

20.3. Нестационарный процесс конвективного теплообмена.

Для нестационарных процессов конвективного теплообмена характерно изменение температур теплоносителей (или одного из них) во времени. Наиболее общим случаем является теплообмен между двумя жидкостями (газами) через стенку, когда изменяются во времени температуры обоих теплоносителей. Например, нагревание или охлаждение жидкости в аппарате (рис. 20.4) с помощью змеевика, через который пропускают другую жидкость (с более высокой или более низкой температурой). Для интенсификации теплообмена жидкость в аппарате обычно перемешивается мешалкой, в результате чего температура ее во всем объеме в данный момент времени одинакова.

Если расход жидкости, протекающей через змеевик G₁, ее удельная теплоемкость с₁, начальная температура (на входе в змеевик) постоянна t_1н = соnst, а конечная (на выходе) t_1к изменяется во времени, при этом t_1к < t_1н, то количество тепла, отданное этой жидкостью за время dτ

                                 .                             (20.10)

Это же тепло перейдет через стенку змеевика к другой жидкости:

                , т.е. ,            (20.11)

где Δt_ср – средняя разность температур жидкостей, переменная во времени.

Температура жидкости в аппарате при теплообмене изменяется от t_2н до t_2к (t_2к > t_2н), ее значение в любой произвольный момент времени t₂. Тогда разность температур жидкостей у входа горячего теплоносителя в змеевик t_1н – t₂, а у выхода t_1к – t₂.

Следовательно, Δt_ср в данный момент