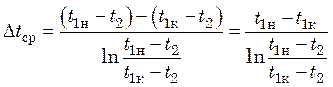Нестационарный теплообмен. Нестационарная теплопроводность. Нестационарный процесс конвективного теплообмена, страница 4

                     .                  (20.12)

Подставив полученное значение Δt_ср в уравнение (20.11), получим

                                     ,

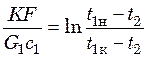откуда 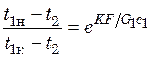                         .                                 (20.13)

Если принять средние значения коэффициента теплопередачи К и удельной теплоемкости с постоянными, то .

Из уравнения (20.13) можно найти переменную конечную температуру жидкости в змеевике:

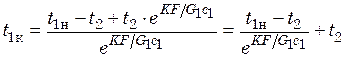                    .                 (20.14)

При подстановке t_1к из уравнения (20.14) в уравнение (20.10) количество переданного тепла dQ выразится равенством

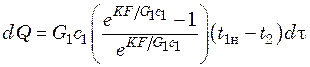                       .                    (20.15)

Это же количество тепла, перешедшее в жидкость в аппарате, можно записать в виде

                                       ,                                    (20.16)

где G₂ и с₂ – количество и удельная теплоемкость жидкости в аппарате, соответственно.

Приравнивая правые части последних уравнений, получим

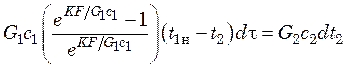                    .                 (20.17)

Разделив переменные и проинтегрировав уравнение(20.17)

                  ,

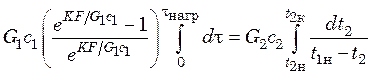найдем время нагревания жидкости в аппарате

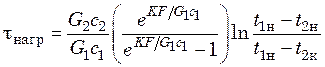                                          (20.18)

либо

                     .

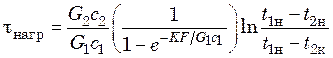Последнее выражение может быть использовано также для определения температуры, до которой нагревается жидкость в аппарате t_2к за время τ_нагр.

Начальную и конечную температуры жидкости в змеевике можно рассчитать, пользуясь уравнением (20.14).

Так, при t₂ = t_2н и разности температур жидкостей t_1н – t_2н

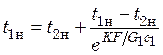                                    .                                (20.19)

При t₂ = t_2к и разности температур t_1к – t_2к

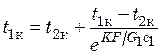                                    .                                (20.20)

Средняя температура жидкости на выходе из змеевика определяется из теплового баланса

                   ,

откуда 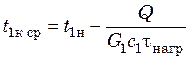                     .                              (20.21)

Приведенный расчет справедлив также и для случая охлаждения жидкости в аппарате. При охлаждении начальная, конечная и средняя температуры охлаждающей жидкости рассчитываются по уравнениям (20.19) – (20.21), соответственно, в которых знак сложения или вычитания изменяется на противоположный.

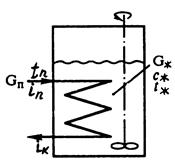
Рисунок 20.5 – К расчету нестационарного теплообмена между
конденсирующимся паром и перемешиваемой жидкостью.

Если температура одного из теплоносителей остается постоянной во времени, расчет процесса нестационарного теплообмена значительно упрощается. Примером может служить нагревание жидкости в аппарате (рис. 20.5) за счет тепла конденсации насыщенного пара (без переохлаждения конденсата) в змеевике.

Начальная температура жидкости в аппарате t_жн, конечная – t_жк. Температура греющего пара – t_п. За промежуток времени dτ количество тепла, переданное паром жидкости через поверхность нагрева F, составит

,

где K – коэффициент теплопередачи; t_ж – температура жидкости в данный момент времени.

Это тепло расходуется на подогрев жидкости

(G_ж, с_ж – количество и удельная теплоемкость жидкости соответственно).

Следовательно,

.

В результате разделения переменных и интегрирования последнего выражения, получим

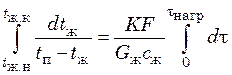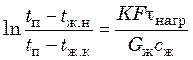            ;   ,        (20.22)

откуда время нагревания жидкости в аппарате от t_жн до t_жк

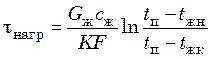                               .                            (20.23)

Уравнение (20.22) может быть использовано также для определения температуры нагреваемой жидкости t_ж в любой момент времени τ:

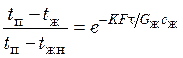                                  .                              (20.24)

Расход греющего пара определяется по тепловому балансу

                          ,                       (20.25)

где G_п – расход пара; r – удельная теплота парообразования.