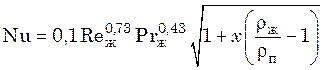 , (23.14)
, (23.14)
где Nu – критерий Нуссельта для пленки конденсата; Reж – критерий
Рейнольдса, рассчитанный по полному расходу парожидкостной смеси и вязкости
жидкой фазы; ![]() – плотности жидкости и пара соответственно;
– плотности жидкости и пара соответственно;
![]() – критерий Прандтля для жидкой фазы.
– критерий Прандтля для жидкой фазы.
Поскольку коэффициенты теплоотдачи являются функциями скоростей движения,
то, чтобы найти их, необходимо знать площади поперечного сечения каналов, по
которым движутся теплоносители (расходы известны). Это требует предварительно
задаться конструкцией и размерами теплообменника. Помимо этого, для вычисления
коэффициента теплоотдачи ![]() часто необходимо знать
температуру стенки
часто необходимо знать
температуру стенки ![]() или удельную тепловую нагрузку
или удельную тепловую нагрузку ![]() , значения которых, в свою очередь, зависят
от определяемой величины
, значения которых, в свою очередь, зависят
от определяемой величины ![]() . В таких случаях коэффициенты
теплоотдачи рассчитывают методом последовательных приближений: величинами
. В таких случаях коэффициенты
теплоотдачи рассчитывают методом последовательных приближений: величинами ![]() и
и ![]() задаются
и после определения величины коэффициента теплопередачи
задаются
и после определения величины коэффициента теплопередачи ![]() проверяют.
Для упрощения расчета можно воспользоваться графоаналитическим методом, при
котором ведут два параллельных расчета для двух выбранных значений
проверяют.
Для упрощения расчета можно воспользоваться графоаналитическим методом, при
котором ведут два параллельных расчета для двух выбранных значений ![]() со стороны одного из теплоносителей.
со стороны одного из теплоносителей.
Так, например, если коэффициенты теплоотдачи ![]() и
и ![]() зависят от температуры стенки
зависят от температуры стенки ![]() , то, задавшись двумя значениями
, то, задавшись двумя значениями ![]() и
и ![]() ,
вычисляют соответствующие значения
,
вычисляют соответствующие значения ![]() и
и ![]() и удельные тепловые нагрузки
и удельные тепловые нагрузки ![]() и
и ![]() :
:
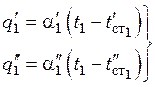 ; (23.15)
; (23.15)
где ![]() –
средняя температура теплоносителя.
–
средняя температура теплоносителя.
По величине термического сопротивления стенки ![]() рассчитывают
температуру стенки со стороны другого теплоносителя:
рассчитывают
температуру стенки со стороны другого теплоносителя:
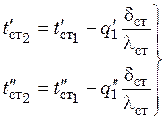 , (23.16)
, (23.16)
и определяют ![]() и
и ![]() , а также
, а также ![]() и
и ![]() :
:
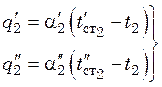 , (23.17)
, (23.17)
(![]() –
средняя температура второго теплоносителя).
–
средняя температура второго теплоносителя).
|
Рисунок 23.1 – Зависимость q1 и q2 от значений tст1. |
Затем строят график зависимости ![]() и
и ![]() от принятых значений
от принятых значений ![]() (рис. 23.1). По точке пересечения
линий, соединяющих тепловые нагрузки при различных значениях
(рис. 23.1). По точке пересечения
линий, соединяющих тепловые нагрузки при различных значениях ![]() , определяют истинные температуру стенки
, определяют истинные температуру стенки ![]() и тепловую нагрузку
и тепловую нагрузку ![]() .
.
Тогда коэффициент теплопередачи ![]() .
.
Величина поверхности теплообмена из общего уравнения теплопередачи
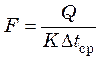 ,
либо
,
либо 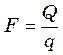 . (23.18)
. (23.18)
Особенности теплового расчета холодильников и конденсаторов. Расчет холодильников-конденсаторов имеет свои особенности, обусловленные характером изменения температур и коэффициентов теплопередачи вдоль поверхности теплопередачи.
На рис. 23.2 показано примерное распределение температур в конденсаторе-холодильнике, в который поступают пары в перегретом состоянии.
В данном случае можно выделить три зоны: I – охлаждение паров до температуры
насыщения; II – конденсация паров и III – охлаждение конденсата. В
первой зоне пары охлаждаются от температуры ![]() до
до ![]() и переходят в насыщенное состояние. Коэффициент
теплопередачи для этой зоны имеет меньшую величину, чем в зоне II, где
происходит конденсация паров. В зоне III коэффициент теплопередачи имеет
промежуточное значение.
и переходят в насыщенное состояние. Коэффициент
теплопередачи для этой зоны имеет меньшую величину, чем в зоне II, где
происходит конденсация паров. В зоне III коэффициент теплопередачи имеет
промежуточное значение.
|
Рисунок 23.2 – Профиль температур |
Тепловой баланс по зонам при условии полной конденсации насыщенного пара
в количестве ![]()
![]() , (23.19)
, (23.19)
где ![]() и
и ![]() – энтальпия перегретого и насыщенного
пара соответственно;
– энтальпия перегретого и насыщенного
пара соответственно; ![]() –удельная теплоемкость
пара;
–удельная теплоемкость
пара;
![]() , (23.20)
, (23.20)
![]() – удельная теплота
парообразования;
– удельная теплота
парообразования;
![]() , (23.21)
, (23.21)
здесь ![]() и
и ![]() – удельная теплоемкость и температура
конденсата.
– удельная теплоемкость и температура
конденсата.
Общая тепловая нагрузка на конденсатор
![]() . (23.22)
. (23.22)
Температуры охлаждающего агента (воды) ![]() в
начале и конце зоны II определяют из уравнений теплового баланса
в
начале и конце зоны II определяют из уравнений теплового баланса
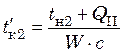 ; (23.23)
; (23.23)
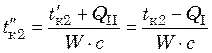 , (23.24)
, (23.24)
(![]() –
удельная теплоемкость охлаждающего агента).
–
удельная теплоемкость охлаждающего агента).
Общий расход охлаждающего агента
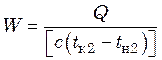 . (23.25)
. (23.25)
Для каждой зоны по известным уравнениям рассчитывают среднюю разность
температур ![]() и коэффициент теплопередачи
и коэффициент теплопередачи ![]() .
.
Тогда поверхности теплообмена зон:
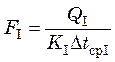 ;
; 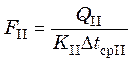 ;
; 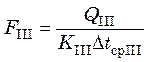 . (23.26)
. (23.26)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.