Основы расчета теплообменных аппаратов. Расчет теплообменников смешения, страница 2

При изменении агрегатного состояния теплоносителя уравнение теплового баланса может иметь различную форму в соответствии с условиями протекания процесса. Например, при конденсации пара

                                                                       (23.4)

( – расход пара;  и  – энтальпии пара и конденсата).

Изменение энтальпии

              ,            (23.5)

где  и  – средние удельные теплоемкости перегретого пара и конденсата;  и  – температуры перегретого и насыщенного пара.

Если неизвестна конечная температура одного из теплоносителей, то ее определяют из теплового баланса. Когда же неизвестны конечные температуры обоих теплоносителей, то для их определения используют общий прием – метод последовательных приближений. Этот метод основан на том, что вначале принимаются определенные решения относительно конструкции аппарата и неизвестных технологических параметров, затем путем пересчета проверяется правильность этого выбора, принимаются уточненные значения указанных параметров и расчет повторяется до получения результатов с желаемой степенью точности. При этом следует принять во внимание, что разность температур между теплоносителями на конце теплообменника должна быть не менее 10–20 °С для жидкостных подогревателей и 5–7 °С для паро-жидкостных подогревателей.

Определение среднего температурного напора  производится с учетом характера изменения температур вдоль поверхности теплообмена . При противотоке, а также при постоянной температуре одного из теплоносителей среднюю разность температур определяют как среднелогарифмическую из большей и меньшей разности температур теплоносителей на концах теплообменника:

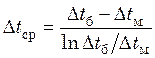                                                                        (23.6)

или при  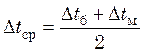    .                                   (23.7)

При всех других схемах течения среднюю разность температур находят по этим же уравнениям, но с введением поправочного коэффициента (см. раздел 19.2).

Среднюю температуру теплоносителя с меньшим перепадом температур по длине аппарата рекомендуется рассчитывать как среднеарифметическую, а среднюю температуру другого теплоносителя находят по известной величине , пользуясь соотношением

                                      ,                                    (23.8)

где  и  – средние температуры теплоносителей.

Дальнейшей задачей расчета является нахождение коэффициента теплопередачи . Если теплопередача происходит через плоскую стенку или тонкую цилиндрическую, то

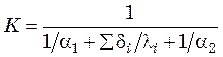                               .                             (23.9)

Для расчета  необходимо предварительно вычислить коэффициенты теплоотдачи  и  по обе стороны теплопередающей стенки, а также термическое сопротивление стенки , которое включает помимо термического сопротивления самой стенки еще и термические сопротивления загрязнений с обеих ее сторон. Термические сопротивления стенки и слоев загрязнений находят в зависимости от их толщины и коэффициентов теплопроводности материала стенки и загрязнений. Коэффициенты теплоотдачи рассчитывают в зависимости от условий теплоотдачи по одному из уравнений, приведенных в разделе 7.6.

Учитывая многообразие гофрированных поверхностей в пластинчатых теплообменниках, Л.Л. Товажнянским и П.А. Капустенко предложена зависимость для расчета коэффициента теплоотдачи, учитывающая угол наклона гофр по отношению к направлению потока рабочей среды:

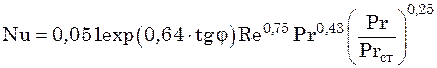             ,         (23.10)

где j – угол наклона гофр.

Это уравнение справедливо в пределах .

Для расчета теплоотдачи в каналах, образуемых пластинами типа 0,3р, 0,6р и 1,0р, уравнение (23.10) может быть представлено в виде:

при

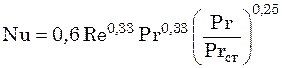                          ;                      (23.11)

при

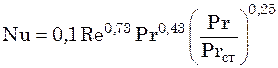                          .                       (23.12)

Теми же авторами предложена формула для расчета теплоотдачи в щелевидных каналах по данным о гидравлическом сопротивлении в диапазоне чисел Рейнольдса Re = 10³–2,5·10⁴ и Прандля Pr = 0,5–20:

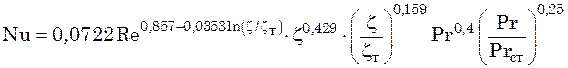, (23.13)

где–коэффициент гидравлического сопротивления щелевидного канала; – коэффициент гидравлического сопротивления гладкой трубы.

При конденсации быстродвижущегося пара (Re > 300) в каналах сетчато-поточного типа Л.Л. Товажнянский и П.А. Капустенко, используя модель движения дисперсно-кольцевого типа, получили следующую зависимость: