


















РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ОТКРЫТЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
КАФЕДРА НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ И ИНЖЕНЕРНОЙ ГРАФИКИ
(САРАТОВСКИЙ ФИЛИАЛ)
ТЕМА: «Разработка организационно-методической системы дистанционного образования по начертательной геометрии
и инженерной графике»
РАЗДЕЛ 1
Разработка структуры электронно-методического пособия по теме: «Позиционные задачи»
Выполнил: ст. препод. Шерлин И.И.
Введение
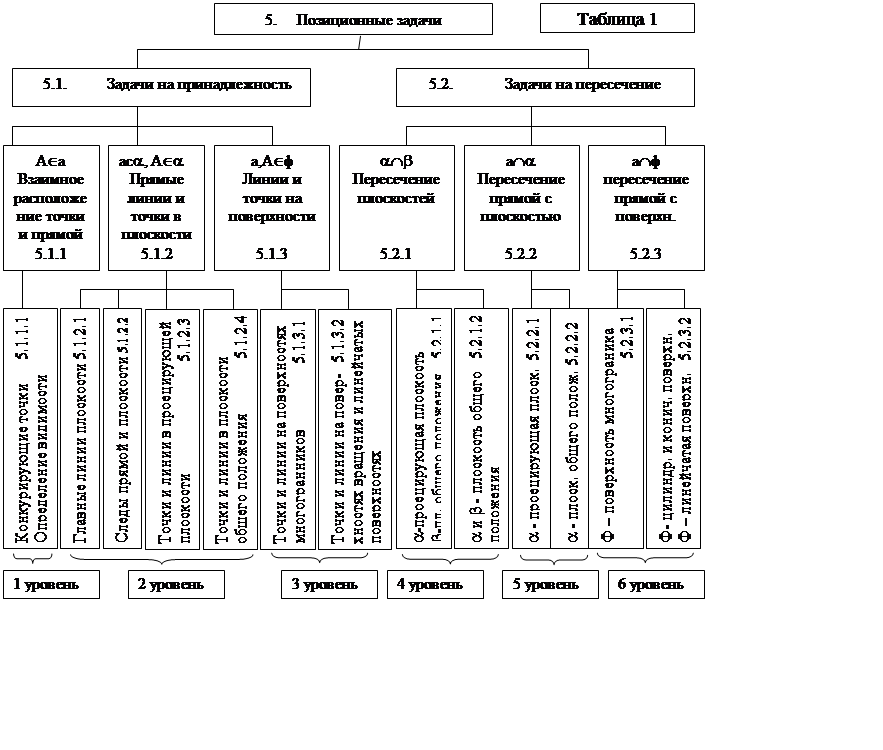
Настоящая глава посвящена позиционным задачам. Позиционные задачи – это задачи на взаимную принадлежность и пересечение фигур. В таблице 1 дано структура изучаемой в настоящей, пятой, главе материала. Позиционные задачи поделены на две группы: первая группа 5.1 – задачи на принадлежность; вторая группа – 5.2. задачи на определение точек пересечения прямой с поверхностью. Каждая группа задач поделена на подгруппы 5.1.1, 5.1.2, 5.1.3 – это соответственно задачи на взаимное расположение точки и прямой, на точку и прямую в плоскости и на поверхности, к этим подгруппам относятся конкретные задачи, так в подгруппе 5.1.2. («прямые линии и точки в плоскости») относятся задачи на тему: «Главные линии плоскости» – 5.1.2.1, «Следы прямой и плоскости» – 5.1.2.2., 5.1.2.3.
В зависимости от сложности, задачи поделены на уровни (см. таблицу 1):
1-й уровень – задачи на взаимное расположение точки и прямой (5.1.1.1.);
2-й уровень – задачи на прямые и точки в плоскости (5.1.2.1…5.1.2.4.);
3-й уровень – задачи на линии и точки на поверхности (5.1.3.1., 5.1.3.2.);
4-й уровень – задачи на пересечение плоскостей (5.2.1., 5.2.1.2.);
5-й уровень – задачи на пересечение прямой с плоскостью (5.2.2.1., 5.2.2.2.);
6-й уровень – задачи на пересечение прямой с поверхностью (5.2.3.1., 5.2.3.2.).
Примеры решения задач даны в настоящем пособии (см. рис. 1-39). Список рекомендуемой литературы дается в конце каждого раздела пособия.
 5.1.1.1
5.1.1.1
Взаимное расположение точки и прямой.
Конкурирующие точки. Определение видимости на эпюре.
Если в пространстве точка принадлежит линии, то проекция этой точки принадлежит проекции этой линии на всех плоскостях проекций; если проекция точки принадлежит проекции линии только на одной плоскости проекций, то в пространстве эта точка не принадлежит линии. Точки, проекции которых совпадают на одной плоскости проекции, называются конкурирующими точками. С помощью этих точек определяется видимость на эпюре, т. е. какая из двух скрещивающихся прямых ближе к нам при проецировании на данную плоскость проекций.
Так на рис.1 изображены скрещивающиеся прямые а и в; точке пересечения фронтальных проекций прямых соответствуют в пространстве две точки 3 и 4 , из которых 3 принадлежит в, а 4 принадлежит а.
Их фронтальные проекции совпадают (32 º 42) потому, что в пространстве обе точки находятся на одном перпендикуляре к плоскости п2. Горизонтальная проекция этого перпендикуляра, обозначена стрелкой (см. рис.1), позволяет установить, какая из двух точек ближе к нам. В нашем случае ближе к нам при проецировании на фронтальную плоскость проекций (вид спереди) будет точка 4. Следовательно, в этом месте прямая а проходит впереди прямой в; таким образом из двух конкурирующих точек, расположенных на одном луче, перпендикулярном плоскости п2, видна будет та точка, горизонтальная проекция которой будет дальше от оси ОХ.
Точке пересечения горизонтальных проекций прямых а и в соответствуют в пространстве так же две точки 1 и 2. Как видно из чертежа точка 1 выше точки 2 и следовательно ближе к нам при проецировании на горизонтальную плоскость проекций. Таким образом, из двух конкурирующих точек на виде сверху (горизонтальная проекция) будет видна та точка, фронтальная проекция которой дальше от оси ОХ.
Задача: Определить видимость ребер АВ и СD (см. рис. 2). Вопрос о видимости на горизонтальной проекции решается с помощью конкурирующих точек 1 и 2; видимым будет ребро ВD, т. к. фронтальная проекция точки 2 принадлежащей ВD, будет дальше от оси ОХ, чем фронтальная проекция точки 1, принадлежащей АС.
 5.1.1.1
5.1.1.1
Вопрос о видимости на фронтальной проекции решается с помощью
конкурирующих точек 3, 4; видимым будет ребро АВ, т. к. горизонтальная проекция точки 4, принадлежащей АВ, будет дальше от оси, чем горизонтальная проекция точки 3, принадлежащей DC.
Рекомендуемая литература.
«Определение видимости на эпюре».
1). Н.Н Крылов «Начертательная геометрия». Москва «Высшая школа » 1990 пар.12 стр. 28.
2). В. О. Гордон «Курс начертательной геометрии». Москва «Высшая школа» 1998 пар. 14 стр. 37.
5.1.2.1
 Прямые линии и точки в плоскости.
Прямые линии и точки в плоскости.
Главные линии плоскости.
1. Горизонтали - прямые лежащие в данной плоскости и параллельные горизонтальной плоскости проекций (см. рис. 3).
Фронтальная проекция горизонтали h2||ОХ.
Горизонтальная проекция горизонтали h2|| aп1
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.