б) уравнение состояния воздуха
; (14.16)
 |
в) уравнение адиабаты
.
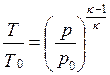(14.17)
Получается
шесть уравнений для шести неизвестных (V, p, ρ, T).
Система приведенных уравнений получила название «уравнения погоды».
Если имеется приток тепла (например, от излучения), то вместо уравнения
адиабаты нужно использовать 
, которое получается из
первого начала термодинамики при dQ ≠ 0. Здесь
все производные - индивидуальные и на самом деле должны быть заменены на 
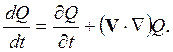Появившаяся новая переменная Q требует дополнительного
уравнения притока тепла для своего определения.
«Уравнения погоды» существенно нелинейны[10], и получить их решение в общем случае невозможно.
[1] Здесь мы рассматриваем несколько упрощенную ситуацию. Более общий случай заключается в том, что имеются три системы координат: основная (инерциальная); система координат с осями, всегда параллельными исходной, движущаяся по отношению к первой; и, наконец, система координат, имеющая общее начало со второй и вращающаяся относительно второй системы. Рассмотрение этого более общего случая не намного сложнее, чем проводимое ниже. Вектор W определяет не только угловую скорость, но и ось, вокруг которой происходит вращение.
[2] В дальнейшем мы практически всюду будем пользоваться горизонтальной системой координат. В этой системе, жестко связанной с вращающейся Землей, начало системы координат находится на поверхности Земли, ось z в данной точке земной поверхности направлена в зенит, ось x – по параллели на восток, ось y – на север). Составляющие вектора скорости вдоль осей обозначаются соответственно.
[3] Жан Бернар Леон Фуко (Foucault, 1819-1868) – французский физик, в 1851 г. осуществил свой знаменитый опыт с маятником.
[4] Выражение (14.7) проще всего получить, если записать полный дифференциал функции : , а затем разделить на .
[5] Например, для x-компоненты скорости имеем
,
откуда и следует приведенное выше соотношение.
[6] В качестве «меток» частицы необязательно использовать ее координаты в какой то момент времени. Можно использовать любые другие характеристики, позволяющие выделить конкретную частицу из других. В частности, иногда в качестве одной из характеристик используют энтропию или, что то же самое, потенциальную температуру. Очевидно, что используемые в качестве «метки» характеристики должны быть независимы друг от друга, и их число для полной идентификации частицы, движущейся в трехмерном пространстве, должно равняться 3. Так, если в качестве одной из «меток» выбрана энтропия, и движение частицы происходит адиабатически, двумя другими «метками» частицы воздуха могут быть две ее координаты в некоторый момент времени на изэнтропической поверхности, по которой происходит движение.
[7] Более детальные сведения о связи формализмов Эйлера и Лагранжа, линий тока и траекторий см. в [51].
[8] В неинерциальной вращающейся системе действует также центробежная сила. Она мала, и её можно учесть, введя коррекцию вектора g с учётом широты местности. При желании, можно также учесть зависимость g от расстояния до поверхности Земли. Все это делается, например, при расчете геопотенциала.
[9] Обозначение указывает, что речь идет о напряжении в плоскости, перпендикулярной оси z, по направлению x.
[10] Нелинейность означает, что уравнения содержат неизвестные величины не только в первой степени. В частности, в нашем случае имеются члены в виде произведения двух неизвестных величин.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.