Уравнения динамики атмосферы. Силы инерции. Уравнение неразрывности. Силы, действующие в атмосфере, страница 7

Всякое изменение количества движения (импульса), согласно второму закону Ньютона, можно рассматривать как результат действия некоторой силы. Очевидно, что эта сила пропорциональна площади соприкосновения двух слоев. Сила трения, отнесенная к единице поверхности, называется напряжением молекулярного трения. Очевидно также, что она должна быть пропорциональна скорости изменения скорости потока в направлении перпендикулярном поверхности[9]:

                                                 .

 Коэффициент пропорциональности η – называется динамическим коэффициентом вязкости.  Отношение ν=η/ρ называют кинематическим (или удельным) коэффициентом вязкости. Размерности названных величин:  [η]=кг/(м·с);  [ν]=м²/с;  [τ_zx]=Н/м². В таблице 14.1 приведены значения коэффициентов вязкости для некоторых случаев [36]. Обратите внимание, что кинематическая (удельная) вязкость воздуха получается намного большей, чем у воды.

Чтобы подсчитать результирующую силу трения, действующую на выделенный объем воздуха, нужно учесть влияние трения со стороны вышележащих и нижележащих слоёв. Пусть объём имеет форму параллелепипеда с основанием 1м² и высотой dz, а поток движется в направлении x (горизонтально). Тогда результирующая сила в направлении x:

                                           .

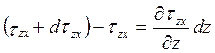На единичный объем получается (делим на dz):

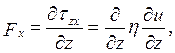
а на единицу массы получим:

                                                        .

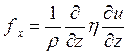Если же скорость u зависит также от x и y (здесь координата  y эквивалентна z, а для координаты x результат получается несколько сложнее), то:

                             .

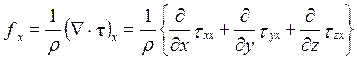Объект τ в виде совокупности 9-ти величин  τ_ij  называют  тензором вязких напряжений. Если величина η = const, то   вектор силы вязкости можно записать следующим образом:

                                                           . 

Здесь оператор Лапласа D действует на каждую компоненту  вектора скорости. Например,

                                         .

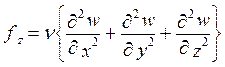Чем меньше масштаб движения (то есть, на меньших расстояниях происходит заметное изменение величины скорости - |V|), тем больше силы трения, тем больше их роль в движении атмосферы. В частности, для крупномасштабных движений, типа общей циркуляции, трением можно пренебречь именно вследствие малости производных ∂²V/∂x², ∂²V/∂y² и, тем более, ∂²V/∂z² для соответствующих масштабов движения.

Масштаб – это не произвольная величина, это характерный размер (длина), на котором движение претерпевает существенные изменения. С учетом турбулентности в реальных воздушных течениях присутствуют  движения различных масштабов. В зависимости от выбора интересующего нас масштаба получается  соответствующая оценка роли молекулярного трения.

Таблица 14.1. Коэффициенты вязкости для некоторых жидкостей и газов

14.5. Уравнения движения

Итак, на воздушную частицу действуют сила тяжести, сила, обусловленная градиентом давления, сила Кориолиса и сила вязкого трения. Согласно 2-му закону Ньютона:

                          .                                                  

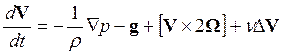Если теперь перейти от индивидуальной производной dV/dt  к локальной, получим

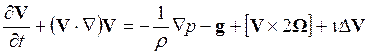                  .                                         (14.14)

К этим трём (для трех составляющих скорости) уравнениям следует добавить:

                     а) уравнение непрерывности для плотности воздуха

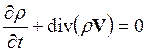                                         ;                                                                           (14.15)