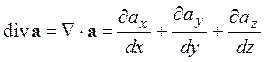Уравнения динамики атмосферы. Силы инерции. Уравнение неразрывности. Силы, действующие в атмосфере, страница 3

                                       .

Уравнение неразрывности (14.6) является следствием закона сохранения массы частицы и выведено на основании этого закона. Формально оно утверждает, что плотность в выделенной частице жидкости (воздуха) изменяется во времени только за счет изменения объема этой частицы. В следующем разделе мы обсудим другой эквивалентный подход к описанию движения жидкости, в рамках которого осуществляется контроль за изменением физических величин в фиксированных точках пространства (метод Эйлера). Тогда уравнение неразрывности интерпретируется несколько иным образом: изменение со временем плотности в заданной точке пространства обусловлено притоком или оттоком жидкости (дивергенцией) в элементарный объем, окружающий эту точку.

Уравнение неразрывности оказывает исключительно важное влияние на особенности движения жидкости и воздуха. Если из какой-то области пространства происходит отток жидкости, то такая ситуация не может продолжаться длительно, поскольку образовавшийся недостаток вещества не позволит продолжать течение, если отсутствует приток вещества из другой области. Именно закон сохранения массы часто обуславливает то, что траектории движения частиц жидкости принимают форму замкнутых циркуляционных ячеек.

14.3. Индивидуальные и локальные производные, метод Лагранжа и метод Эйлера изучения движения воздуха

Рассмотрим некоторую физическую величину q, характеризующую индивидуальную воздушную частицу (объем малых, но макроскопических размеров, в пределах которого все характеристики воздуха можно считать неизменными). Очевидно, что , то есть, содержание физической величины в частице зависит от ее положения в пространстве и от времени. Поскольку частица движется, её координаты также являются функциями времени:. Изменение величины q со временем внутри воздушной частицы будем характеризовать производной dq/dt. Для сложной функции имеем[4]:

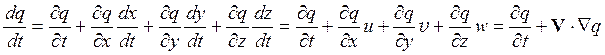             ,            (14.7)

где использовано определение вектора скорости  (r – радиус-вектор частицы) и его проекций на оси координат. Здесь также введена операция градиента, grad или , определяемая соотношениями:

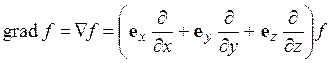                                           .                                       (14.8)

Производную dq/dt, характеризующую скорость изменения физической величины q в движущейся воздушной частице, называют индивидуальной или полной производной. Частную производную, по смыслу представляющую собой изменение q в неподвижной точке пространства с координатами x, y, z, называют локальной или местной производной.

Согласно вышеприведенной формуле (14.7), изменение со временем физической величины q в точке пространства с координатами x, y, z  () складывается из изменения со временем величины q в частице, находящейся в данный момент в рассматриваемой точке  (), и различия в величинах q в частицах, приходящих в эту точку: ().

Например, температура T воздуха в данной точке пространства  может изменяться вследствие поглощения или испускания излучения. Этот эффект характеризуется скоростью изменения температуры в частицах воздуха в окрестности данной точки пространства – производной  . Однако та же температура может меняться из-за того, что в данную точку с воздушным течением приходят более теплые или более холодные частицы. Этот эффект характеризуется членом  . Производные  называют еще пространственными или геометрическими.

В качестве другого примера рассмотрим задачу об определении ускорения частицы жидкости в ходе движения. Пусть в момент времени t положение частицы характеризовалось вектором r, а скорость – вектором V(r,t). В момент времени t+Δt  соответственно имеем r+Δr, V(r+Δr,t+Δt), поскольку частица переместилась в другое положение (с точностью до членов первого порядка малости Δr≈V(r,t)Δt). Тогда, ограничиваясь членами первого порядка малости, находим с учетом определения частных производных[5]