С достаточной степенью точности для изучения атмосферных движений оказывается инерциальной система координат, движущаяся вокруг Солнца вместе с Землей, но не вращающаяся вместе с Землей вокруг ее оси. Однако и она не слишком удобна для использования, поскольку мы привыкли рассматривать атмосферные движения по отношению к покоящейся Земле, то есть, рассматривать относительные движения, относительные скорости и относительные ускорения в системе координат, вращающейся вместе с Землей. В качестве такой системы обычно выбирают так называемую горизонтальную систему координат[2]. Тогда в правую часть уравнения для относительного ускорения следует ввести поправочные члены, обусловленные неинерциальностью системы отсчета.
Эти поправочные члены называют силами инерции, а именно, центробежной силой и силой Кориолиса. Будучи отнесенными к единице массы, они численно равны соответственно второму и третьему слагаемым в (14.5), взятым с обратным знаком. С учетом введенных сил инерции относительное ускорение материальной точки получается отличным от нуля, несмотря на отсутствие реальных действующих сил, а относительная траектория получается криволинейной (хотя она прямолинейна в инерциальной гелиоцентрической системе отсчета). Классическим примером, демонстрирующим эффекты неинерциальности системы отсчета, скрепленной с Землей, является маятник Фуко[3].
В дальнейшем
уравнения движения будут рассматриваться, как правило, в системе координат,
вращающейся вместе с Землей. При этом для производной по времени мы будем
использовать обычное обозначение - ![]() , не забывая, однако,
что речь идет об относительном движении, и о необходимости учета сил инерции.
, не забывая, однако,
что речь идет об относительном движении, и о необходимости учета сил инерции.
Центробежная сила там, где она имеет наибольшие значения (вблизи экватора, где велико расстояние до оси вращения), близка по направлению к силе тяжести, составляет малую долю по сравнению с ней и может быть учтена посредством незначительной коррекции вектора силы тяжести. Поэтому в дальнейшем практически всюду мы не будем специально выделять эту силу.
Сила Кориолиса зависит от величины и направления скорости относительного движения и может существенно влиять на последнее. Поэтому она, как правило, всегда будет явно присутствовать в уравнениях относительного движения.
Приведенные соотношения вполне достаточны для рассмотрения атмосферных движений. Тем не менее, их легко обобщить на более сложные случаи, когда начало вращающейся системы отсчета перемещается в пространстве, и вектор угловой скорости вращения меняет величину и направление.
Рассмотрим
элементарную частицу жидкости или газа массой dm, заполняющую объём dt. Если проследить поведение во времени
данной частицы, то неизменность ее массы можно выразить соотношением: ![]() . Но dm=rdt, где
r
- плотность. Поэтому
. Но dm=rdt, где
r
- плотность. Поэтому
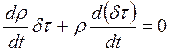 .
.
Пусть dt - параллелепипед
с размерами Dx,
Dy, Dz. По
истечении времени Dt
длины сторон изменятся. Действительно, пусть вдоль оси х координаты
начала и конца объема в нулевой момент времени были ![]() . Компоненты вектора скорости вдоль осей горизонтальной системы координат обозначаются u,
. Компоненты вектора скорости вдоль осей горизонтальной системы координат обозначаются u, ![]() ,
w. Тогда через интервал времени ∆t объем
переместится в новое положение:
,
w. Тогда через интервал времени ∆t объем
переместится в новое положение:
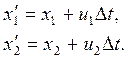
Аналогичным образом изменятся y, z-координаты.С точностью до членов первого порядка малости по ∆t имеем
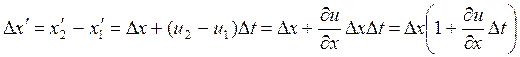 .
.
Отсюда
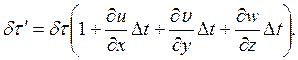
Следовательно,
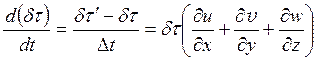 .
.
Окончательно получаем:
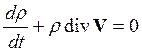 .
(14.6)
.
(14.6)
Напомним, u, v, w – составляющие вектора скорости:
![]() ,
,
а векторы ![]() -
единичные орты осей
-
единичные орты осей ![]() горизонтальной системы
координат. Операция div называется
дивергенцией и определена следующим образом:
горизонтальной системы
координат. Операция div называется
дивергенцией и определена следующим образом:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.