Уравнения динамики атмосферы. Силы инерции. Уравнение неразрывности. Силы, действующие в атмосфере, страница 5

В подавляющем большинстве случаев задачи о движении воздуха решаются в переменных Эйлера. Соотношение (14.7) справедливо для любой физической величины. Процедуру перехода от индивидуальных производных к локальным (и наоборот) можно осуществить, используя операторное равенство:

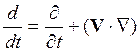                                        .                                                                   (14.9)

Преобразуем уравнение неразрывности к переменным Эйлера:          

                     .                       (14.10)

Следовательно

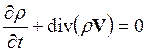                                              .                                                                      (14.11 )

Это уравнение показывает, что скорость изменения плотности в заданной точке пространства определяется притоком или оттоком вещества в окрестность выбранной точки. Другими словами говорят, что скорость изменения плотности в точке определяется дивергенцией плотности потока массы .

Оценки порядков величин производных, фигурирующих в уравнении неразрывности, показывают, что  часто в реально наблюдаемых процессах временные производные по порядку величины заметно меньше пространственных производных. Тогда уравнение (14.11) приближенно можно записать в виде

                                                                 .                                                            (14.12)

Наконец, иногда в задачах динамики атмосферы оказывается допустимым приближение несжимаемой жидкости. Тогда уравнение неразрывности приобретает вид

                                                                 .                                                               (14.13)

Приближение несжимаемой жидкости допустимо, когда изменение плотности в данной точке пространства со временем и изменение плотности при переходе от одной точки пространства к соседней незначительны по сравнению с изменением скорости в пространстве. Оказывается, такое приближение иногда вполне приемлемо при рассмотрении движений в атмосфере со скоростями, значительно меньшими скорости распространения звука. Оно  совершенно не годится, когда исследуется распространение звуковых волн в воздухе.

В заключение коротко остановимся на понятии линии тока. Линия тока определяется тем, что касательная в каждой точке ее совпадает с направлением скорости в этой точке в заданный момент времени. Обратите внимание, здесь ничего не говорится о величине скорости. Следовательно, величина скорости вдоль линии тока может меняться. Исходя из определения, уравнение линии тока имеет вид  (приращение элемента линии тока пропорционально скорости  в заданный момент времени). Здесь - скалярный параметр. Время в приведенных уравнениях  играет роль параметра, значение которого определяет разные линии тока, проходящие через точку с координатами x,y,z в разные моменты времени. Поскольку величина и направление скорости в общем случае зависят от времени, линии тока дают представление о распределении направлений скоростей движения только для одного определенного момента времени. Поэтому линии тока совпадают с траекториями частиц только в случае установившегося движения, когда скорости не зависят от времени. Приведенные выше уравнения линий тока можно также записать в виде

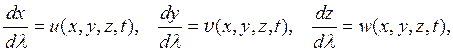
в то время как уравнения траекторий имеют вид

                      .

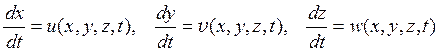Дифференциальные уравнения траекторий частиц имеют такой же вид, как и уравнения линий тока, однако время теперь не является параметром, а служит независимой переменной. Очевидно, что вектор скорости является касательной к каждой точке траектории в последовательные моменты времени, соответствующие прохождению частицы через эти точки[7].

14.4. Силы, действующие в атмосфере

Градиент давления и сила тяжести