Тема:Корреляционный и регрессионный анализ
1. Линейная регрессия
Линейная зависимость признака y от признака x определяется формулой: y = α + β∙x. Коэффициент α определяет координату точки пересечения прямой с осью Y; его называют также коэффициентом сдвига. Коэффициент β называют коэффициентом наклона. Сама линия называется прямой регрессии.
Выборочные оценки обозначим a и b. Формулы для расчета коэффициентов уравнения регрессии:
- коэффициент сдвига:
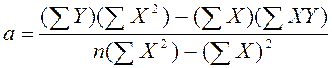
- коэффициент наклона:
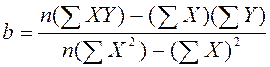
где X, Y – значения переменных для n членов выборки. Вычисления можно упростить, если сначала вычислить b, а затем найти a по формуле:
![]() .
.
При каждом X существует разброс значений Y со стандартным отклонением σY|X. Выборочной оценкой σY|X служит остаточное стандартное отклонение sY|X, которое вычисляется по формуле:
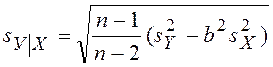 ,
,
где sX, sY – стандартные отклонения X и Y.
Стандартные ошибки коэффициентов регрессии рассчитываются по следующим формулам:
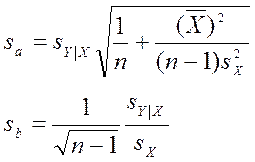
Для проверки статистической значимости линейной зависимости можно воспользоваться критерием Стьюдента:
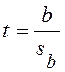 .
.
Найдем tα – критические значения t для уровня значимости α и числа степеней свободы ν = n–2. Если |t|>tα, то зависимость статистически значима.
Условия применимости регрессионного анализа:
1) линейность связи переменных; перед тем как приступить к расчетам, необходимо нанести данные на график;
2) нормальность распределения;
3) изучаемые признаки должны быть количественными.
Пример. Построить графики для приведенных наборов данных. Найти коэффициенты уравнения регрессии и проверить статистическую значимость найденной линейной зависимости.
Перед началом регрессионного анализа следует нанести данные на график, чтобы убедиться в линейной зависимости. Выберите Тип диаграммы – Точечная; в качестве диапазона данных укажите диапазон, в котором содержатся данные по Х и У (в приведенном ниже примере А1:В9). Далее в меню Диаграмма выберите Добавить линию тренда…(тип линейная). На вкладке Параметры отметьте флажками Показывать уравнение на диаграмме и Поместить на диаграмму величину достоверности аппроксимации.
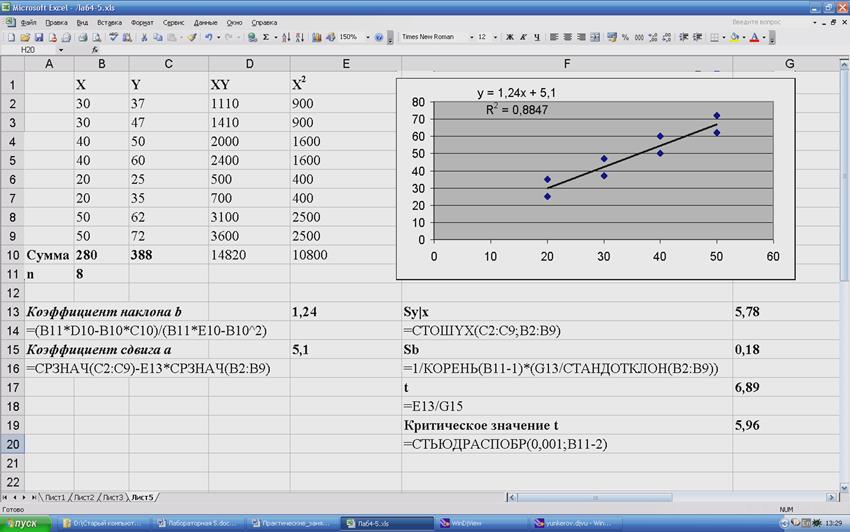
Критическое значение t меньше рассчитанного. Таким образом, коэффициент наклона является статистически значимым.
Задание 1. Проведите вышеуказанные вычисления для следующего набора данных. Как повлияло увеличение объема выборки на коэффициенты уравнения регрессии и статистическую значимость линейной зависимости?
|
X2 |
Y2 |
|
30 |
37 |
|
30 |
47 |
|
40 |
50 |
|
40 |
60 |
|
20 |
25 |
|
20 |
35 |
|
50 |
62 |
|
50 |
72 |
|
10 |
13 |
|
10 |
23 |
|
60 |
74 |
|
60 |
84 |
Задание 2. Постройте графики для двух наборов данных. Найдите для каждого линию регрессии (с помощью меню Диаграмма). Нанесите полученные прямые регрессии на графики с исходными данными. Почему получились такие результаты? Выполнены ли условия применимости регрессионного анализа; можно ли для второй выборки выразить связь единственной линией регрессии?
|
Х1 |
Y1 |
X2 |
Y2 |
|
15 |
19 |
20 |
21 |
|
15 |
29 |
20 |
31 |
|
20 |
25 |
30 |
18 |
|
20 |
35 |
30 |
28 |
|
25 |
31 |
40 |
15 |
|
25 |
41 |
40 |
25 |
|
30 |
37 |
40 |
75 |
|
30 |
47 |
40 |
85 |
|
60 |
40 |
50 |
65 |
|
50 |
75 |
||
|
60 |
55 |
||
|
60 |
65 |
Использование пакета Анализ данных.
Пакет Анализ данных позволяет выполнять регрессионный анализ. В меню Сервис выберите команду Анализ данных. Выберите в диалоговом окне Анализ данных функцию Регрессия и нажмите кнопку ОК. Установите параметры анализа в соответствующем диалоговом окне.
- Входной интервал Y и входной интервал Х;
- Отметьте флажком Метки, если в первых ячейках находятся заголовки столбцов;
- Параметры вывода: укажите первую ячейку для вывода результатов.
Результат применения пакета анализа выглядит следующим образом:
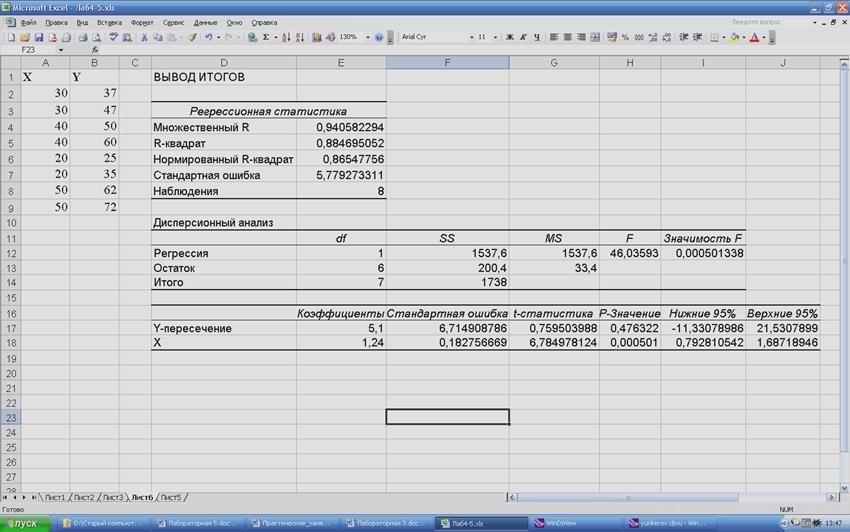
Значения коэффициента сдвига а, его ошибки и доверительные интервалы приведены в строке Y-пересечение. Значения коэффициента наклона b, его ошибки и доверительные интервалы приведены в строке X. По коэффициенту детерминации R2 модель можно считать информативной. Фактор X на 88,47% объясняет дисперсию параметра Y. По уровню значимости p=0,0005 модель является значимой.
Задание 3. Проведите вышеуказанные вычисления для данных из задания 1.
Задание 4. Исследуется связь между поглощенной дозой облучения, Гр (Y) и долей аберрантных клеток костного мозга, % (Х) у 15 подопытных животных (белые мыши). Результаты приведены в таблице. С помощью пакета анализа вычислите коэффициенты уравнения линейной регрессии и оцените статистическую значимость коэффициента наклона b.
|
Х Доля аберрантных клеток костного мозга, % |
Y Доза облучения, Гр |
|
59 |
3,2 |
|
44 |
2,5 |
|
85 |
4,5 |
|
70 |
4,0 |
|
52 |
3,0 |
|
21 |
0,8 |
|
26 |
1,3 |
|
79 |
4,0 |
|
41 |
3,1 |
|
67 |
3,5 |
|
32 |
1,8 |
|
18 |
0,7 |
|
90 |
4,3 |
|
12 |
0,3 |
|
100 |
5,0 |
Задание 5. В таблице представлены результаты трех экспериментов. Нанесите результаты на график. Вычислите коэффициенты линейной регрессии для того эксперимента, где выполняются условия применимости регрессионного анализа.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.