Тема:Анализ качественных признаков
(Критерий χ2. Сравнение долей.)
Критерий χ2 – это непараметрический критерий, является аналогом дисперсионного анализа для качественных признаков.
По имеющимся данным исследования строят таблицу сопряженности. Строки таблицы представляют собой сравниваемые факторы, а столбцы - возможные исходы эксперимента. Подсчитывают число объектов в каждой строке и каждом столбце. Наблюдаемые значения обозначают буквой О (observed). Таблица сопряженности выглядит следующим образом (Ri – суммы в строках таблицы, Cj – суммы в столбцах таблицы, N – общий объем исследования, r-число строк, c-число столбцов):
|
О11 |
О12 |
… |
O1c |
R1 |
|
О21 |
О22 |
… |
O2c |
R2 |
|
… |
… |
… |
… |
… |
|
Or1 |
Or2 |
… |
Orc |
Rr |
|
C1 |
C2 |
… |
Cc |
N |
Далее подсчитывают с точностью до двух знаков после запятой ожидаемые числа – количество объектов, которое попало бы в каждую клетку, если бы изучаемые факторы не влияли бы на исход. Ожидаемые значения обозначают буквой E (expected). Таблица ожидаемых чисел рассчитывается следующим образом (обратите внимание, что суммы по строкам и столбцам должны сохраниться):
|
E11=R1∙C1/N |
E12=R1∙C2/N |
… |
E1c=R1∙Cc/N |
R1 |
|
E21=R2∙C1/N |
E22=R2∙C2/N |
… |
E2c=R2∙Cc/N |
R2 |
|
… |
… |
… |
… |
… |
|
Er1=Rr∙C1/N |
Er2=Rr∙C2/N |
… |
Erc=Rr∙Cc/N |
Rr |
|
C1 |
C2 |
… |
Сс |
N |
По полученным таблицам рассчитывается значение критерия:
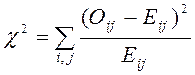 ,
,
где Оij – наблюдаемые значения в клетках таблицы, Еij – ожидаемые значения. Суммирование производится по всем клеткам таблицы.
Применение критерия χ2 правомерно, если ожидаемые числа в любой из клеток больше либо равны 5.
Число степеней свободы ν=(r-1)(c-1).
В случае таблицы 2×2 в формулу вводят поправку Йейтса:
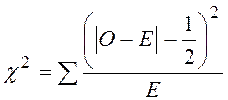 .
.
Пример. Изучение влияния дополнительного приема эстрогена на риск развития болезни Альцгеймера. В исследовании принимала участие группа из 1124 пожилых женщин, 156 из которых длительное время получали эстроген. Группа наблюдалась в течение пяти лет, регистрировались случаи болезни Альцгеймера. Результаты расчетов:
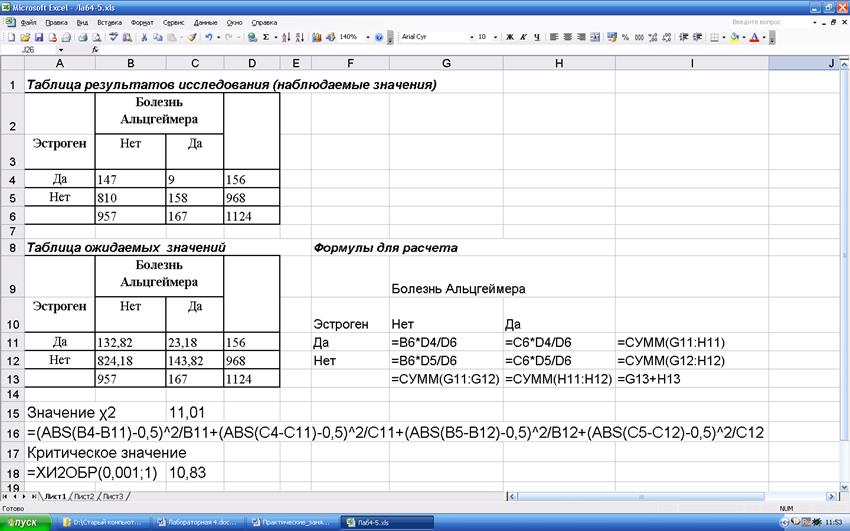
Рассчитанное значение больше критического, поэтому можем утверждать, что дополнительный прием эстрогена снижает риск развития болезни Альцгеймера (вероятность ошибки менее 0,1%).
Задание 1
1. Синдром внезапной детской смерти — основная причина смерти детей в возрасте от 1 недели до 1 года. Обычно смерть наступает на фоне полного здоровья незаметно, во сне, поэтому определение факторов риска имеет первостепенное значение. Исследователи собрали сведения о 18 955 детях, родившихся в одном из роддомов Окленда, штат Калифорния, с 1960 по 1967 г. Судьбу детей проследили до 1 года. От синдрома внезапной детской смерти умерли 44 ребенка. Данные о предполагаемых факторах риска представлены в таблице. Найдите признаки, связанные с риском синдрома внезапной детской смерти (два по выбору). По некоторым признакам данные отсутствуют, поэтому сумма в третьем столбце может оказаться меньше 44, а в четвертом — меньше 18955.
|
Фактор |
Синдром |
||
|
Да |
Нет |
||
|
Возраст матери |
До 25 лет 25 лет и старше |
29 15 |
7301 11241 |
|
Время от окончания предыдущей беременности |
Менее 1 года Более 1 года |
23 11 |
4694 7339 |
|
Планировалась ли беременность |
Нет Да |
23 5 |
7654 4253 |
|
Курение во время беременности |
Да Нет |
24 10 |
5228 9595 |
|
Низкий гемоглобин во время беременности |
Да Нет |
26 7 |
12613 2678 |
|
Раса |
Белые Негры Другие |
31 9 4 |
12240 4323 2153 |
1.2. Проводилась оценка эффективности терапии для лечения синдрома хронической обеспокоенности. В исследовании принимало участие 150 человек, 60 из которых получали двухмесячную программу лечения. После двух месяцев проводилась оценка состояния (ухудшилось, улучшилось, не изменилось). Результаты в таблице:
|
Терапия |
Состояние |
|||
|
Ухудшилось |
Не изменилось |
Улучшилось |
||
|
Да |
24 |
11 |
25 |
60 |
|
Нет |
30 |
31 |
29 |
90 |
|
54 |
42 |
54 |
150 |
|
Есть статистически значимые различия между группами? Что произойдет, если удвоить количество участников эксперимента при сохранении пропорций между группами? Рассчитайте.
Пусть имеется выборка из n объектов, при
этом m из них обладает каким-то качественным признаком,
которого нет у остальных n-m объектов. Тогда доля объектов, выборки, обладающих
признаком, вычисляется как p=m/n. Показатель разброса значений – стандартное
отклонение доли – вычисляется по формуле: ![]() ;
стандартная ошибка доли:
;
стандартная ошибка доли: 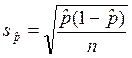 .
.
Критерий z для проверки нулевой гипотезы о равенстве долей в двух выборках:
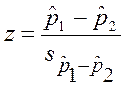
где
![]() - выборочные доли,
- выборочные доли, ![]() -
стандартная ошибка разности долей.
-
стандартная ошибка разности долей.
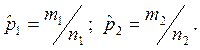 Объединенная оценка
доли:
Объединенная оценка
доли: 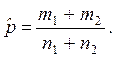
Стандартная ошибка разности долей вычисляется:
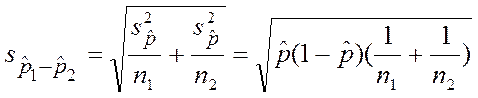 .
.
Для нахождения критических значений z необходимо воспользоваться таблицами значений стандартного нормального распределения. При увеличении числа степеней свободы распределение Стьюдента стремится к нормальному, поэтому критические значения z можно найти в последней строке таблицы распределения Стьюдента. Для α =0,05 z0,05=1,96; для α=0,01 z0,01=2,58.
С учетом этой поправки Йейтса формула для расчета z имеет вид:
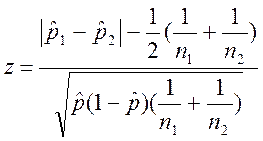 .
.
Пример. Применим z-критерий для задачи о влиянии дополнительного приема эстрогена на риск развития болезни Альцгеймера. В группе принимавшей эстроген (n1=156) количество заболевших составило 9 (m1=9). Во второй группе (n2=968) количество заболевших составило 158 (m2=158).
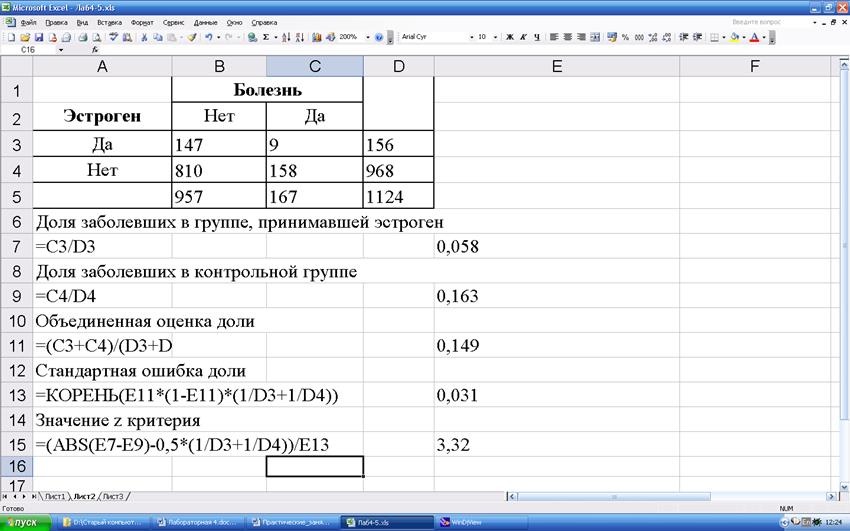
Рассчитанное значение больше, чем z0,01. Поэтому с уровнем значимости 0,01 можем утверждать, что между долями заболевших существуют статистически значимые различия.
Задание 1
Исследовалось влияние экзогенных стероидных гормонов во время беременность у 108 матерей детей с врожденными дефектами. Непреднамеренное использование оральных контрацептивов на ранних сроках беременности рассматривалось как основной фактор воздействия. У матерей больных детей отмечено употребление контрацептивов в 15 случаях, в контрольной группе (также 108 матерей) – в 4 случаях. Есть ли статистически значимые различия между группами?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.