Тема:Непараметрические методы
1. Критерий Манна-Уитни
Является аналогом критерия Стьюдента для независимых выборок. Для его применения необходимо упорядочить значения для обеих групп вместе, заменить значения рангами, а затем найти сумму рангов для каждой группы.
Критические значения критерия Манна-Уитни приводятся в специальной таблице (см. Таблицу 5 Приложения). В ней задается численность групп (меньшей и большей). Столбец критических значений содержит пары чисел Т1 и Т2. Если сумма рангов меньшей группы Тменьш не больше первого из них или не меньше второго (т.е. Тменьш ≤ Т1 или Тменьш ≥ Т2), то различия статистически значимы.
При численности групп больше 8 распределение суммы рангов приближается к нормальному со средним значением:
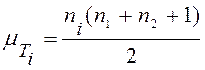
и стандартным отклонением:
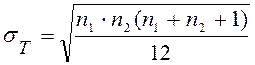 ,
,
где i – номер группы, ni – численность группы. В таком случае величина
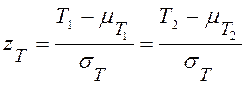
имеет стандартное нормальное распределение. Рассчитанное значение сравнивают с критическими значениями стандартного нормального распределения (последняя строка таблицы Стьюдента). Более точный результат обеспечивает поправка на непрерывность.
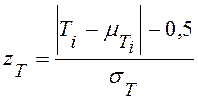 .
.
Пример. Группа количеством 21 человек, нуждающихся в лечении клаустрофобии, была случайным образом разделена на две подгруппы: n1=11 и n2=10. Члены первой группы получали лечение одного типа, второй – другого типа. В конце исследования независимая группа экспертов оценила поведение пациентов в стрессовых ситуациях клаустрофобии по 10-балльной шкале: 1 – очень низкий уровень клаустрофобии, 10 – очень высокий. В таблице приведены средние значения оценок для каждого пациента. Является ли лечение первого типа более эффективным?
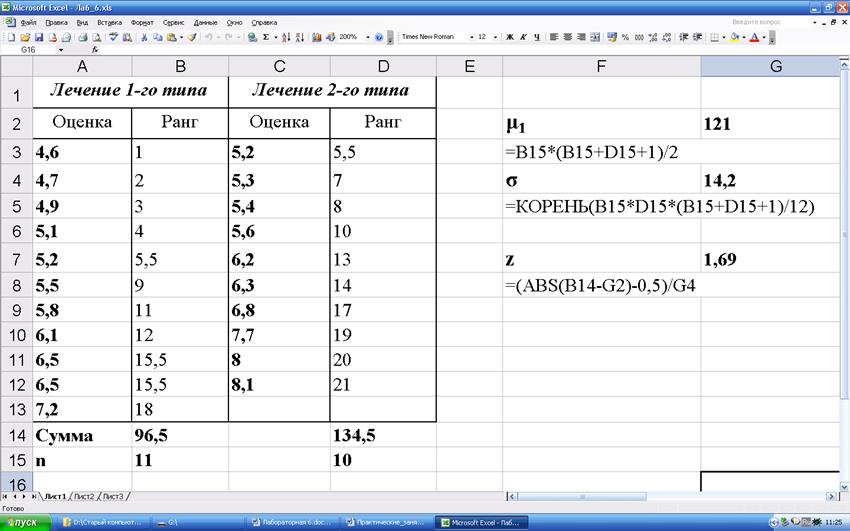
Критическое значение z для уровня значимости 0,05 составляет 1,96, что больше рассчитанного значения. Таким образом, между группами нет статистически значимых различий и нельзя говорить о превосходстве какого-либо метода лечения.
Задание 1.
|
|
Экстракт от крыс с циррозом |
||
|
|
80 |
||
|
1000 |
80 |
||
|
1370 |
80 |
||
|
1680 |
210 |
||
|
1970 |
210 |
||
|
2420 |
320 |
||
|
3260 |
500 |
||
|
5000 |
610 |
||
|
5400 |
760 |
||
|
7370 |
760 |
||
|
890 |
|||
|
890 |
|||
|
1870 |
|||
|
1950 |
Какой вывод можно сделать по результатам опыта?
2. Критерий Уилкокосона
Является непараметрическим аналогом парного критерия Стьюдента. Принцип критерия: для каждого члена выборки вычисляют величину изменения признака. Все изменения упорядочивают по абсолютной величине (без учета знака). Затем рангам приписывают знак изменения и суммируют их. В результате получается значение критерия Уилкоксона – W.
Если значения первого и второго измерений для члена выборки совпадают, т.е. изменение признака равно нулю, то такую пару значений исключают из дальнейшего рассмотрения, при этом объем выборки уменьшается на единицу.
Критические значения W находят по специальной таблице для критерия Уилкоксона, в зависимости от объема выборки (Таблица 6 Приложения). Если рассчитанное значение по абсолютной величине меньше критического, то изменения не являются статистически значимыми.
При n>20 распределение W достаточно близко к нормальному со средним значением μW=0 и стандартным отклонением, которое вычисляется по формуле:
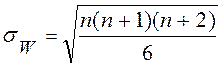 .
.
Далее
рассчитывают значение zW=![]() ,
которое имеет стандартное нормальное распределение. Вычисленное значение
сравнивают с критическими значениями стандартного нормального распределения.
Более точный результат обеспечивает поправка на непрерывность: zW=
,
которое имеет стандартное нормальное распределение. Вычисленное значение
сравнивают с критическими значениями стандартного нормального распределения.
Более точный результат обеспечивает поправка на непрерывность: zW=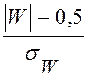 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.