Непараметрические методы (Лабораторная работа № 6), страница 2

Пример. Студенты отвечают на вопросы по теории вероятностей. Им нужно оценить вероятность события в каждом вопросе по шкале от 0 до 100%. Преподавателя интересуют ответы на вопросы А и В, т.к студенты, которые хорошо усвоили курс, должны были оценить вероятность события в вопросе А выше, чем в вопросе В. Результаты приведены в таблице. Для удобства ответы уже упорядочены по возрастанию абсолютной величины разности между ними.

Большая часть студентов действительно оценила вероятность события в вопросе А выше. Но будут ли эти различия статистически значимыми?

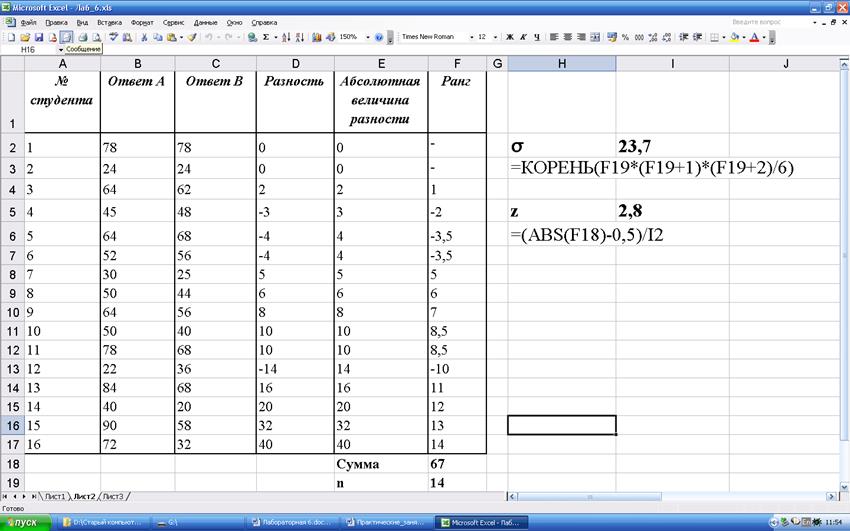
Z = 2,8 > 2,58 (критическое значение для уровня 0,01) – различия статистически значимы.

Задание 2.

Психолог проводит групповой тренинг. Его задача – выяснить, будет ли эффективен данный вариант тренинга для снижения уровня тревожности участников. Для решения этой задачи с помощью специальной шкалы был дважды выявлен уровень тревожности у 17 участников до и после проведения тренинга. Результаты приведены в таблице.

Можно ли утверждать, что после тренинга наблюдается уменьшение уровня тревожности участников? 

Задание 3.

Исследование влияния курения на агрегацию тромбоцитов. 11 добровольцам было предложено  выкурить по сигарете. Перед курением и сразу после него были взяты пробы крови и определена агрегация тромбоцитов. Результаты в таблице:

3.  Критерий Крускала-Уоллиса

Является непараметрическим аналогом дисперсионного анализа. Сначала все значения объединяют и упорядочивают по возрастанию. Каждому значению присваивается ранг. Затем вычисляют суммы рангов, относящихся к каждой группе, и для каждой группы вычисляют средний ранг.

Значением критерия Крускала-Уоллиса является величина:

,

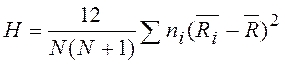где

R_i – сумма рангов в i-ой группе; n_i – численность этой группы;

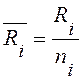 - средний ранг в i-ой группе;

- общая численность исследования,  - средний ранг для объединенной группы: .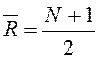

Если группы не слишком малы, то распределение H хорошо приближается распределением χ² с числом степеней свободы ν=k–1 (k – количество групп). В случае трех групп это применимо, если численность каждой группы не меньше пяти. Для четырех групп – если общая численность исследования не меньше десяти. Для меньших объемов исследования существует таблица значений критерия Крускала-Уоллиса (таблица 7 Приложения).

Пример. При заболеваниях сетчатки повышается проницаемость ее сосудов. В исследовании сравнивалась проницаемость сосудов сетчатки в трех группах: у здоровых людей (n₁=12); у больных с поражениями сетчатки преимущественно в области центра (n₂=12); у больных с аномалиями и в центре, и на периферии (n₃=9). Результаты приведены в таблице. Различается ли проницаемость сосудов сетчатки в этих группах статистически значимо?

Замечание!!! Для расстановки рангов следует скопировать все значения по трем группам в один массив, упорядочить его, присвоить значениям ранги, а затем расставить ранги в исходную таблицу

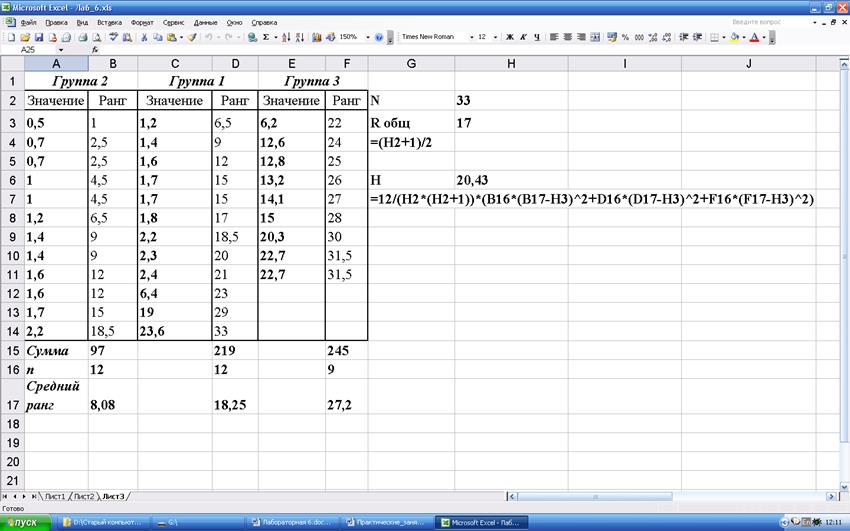
Табличное значение χ² для двух степеней свободы и уровня значимости 0,01 составляет 9,21. Рассчитанное значение H больше, поэтому делаем вывод о статистической значимости различий между группами.

Задание 4.

При поражении левой коронарной артерии кровоснабжение левого желудочка ухудшается. В покое это никак не проявляется, однако при физической нагрузке это приводит к накоплению крови в легких. При поражении правой коронарной артерии этого не происходит. Для подтверждения этой гипотезы было обследовано 33 человека: 9 здоровых (1-я группа) и 24 больных ишемической болезнью сердца, из них 5 с поражением только правой коронарной артерии (2-я группа) и 15 с поражением обеих коронарных артерий или только левой (3-я группа). Рассчитывали отношение кровенаполнения легких при физической нагрузке к кровенаполнению в покое. В 3-й группе этот показатель должен быть выше, чем в первых двух. Результаты представлены в таблице. Различаются ли группы между собой?