Тема: «Дисперсионный анализ»
Дисперсионный анализ позволяет проверить гипотезу о равенстве средних в нескольких группах. Для k групп с равной численностью n значение критерия F может быть вычислено по формуле:
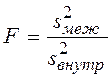 .
.
![]() – межгрупповая
дисперсия, где n – объем выборок,
– межгрупповая
дисперсия, где n – объем выборок, ![]() - дисперсия выборки,
составленной из выборочных средних.
- дисперсия выборки,
составленной из выборочных средних.
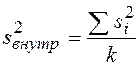 – внутригрупповая
дисперсия, где k – количество групп, si2- выборочные оценки дисперсии в группах. Межгрупповое
число степеней свободы νмеж=k-1, где k-число
групп. Внутригрупповое число степеней свободы νвнутр=k(n-1),
где n – численность каждой группы.
– внутригрупповая
дисперсия, где k – количество групп, si2- выборочные оценки дисперсии в группах. Межгрупповое
число степеней свободы νмеж=k-1, где k-число
групп. Внутригрупповое число степеней свободы νвнутр=k(n-1),
где n – численность каждой группы.
Обобщение на случай групп с произвольной численностью. Пусть имеется k групп, ni
– численность i-ой группы, ![]() -
среднее в i-ой группе, si2 – дисперсия в i-ой группе,
-
среднее в i-ой группе, si2 – дисперсия в i-ой группе, ![]() -
общий объем исследования. Тогда:
-
общий объем исследования. Тогда:
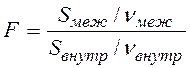
где ![]() - это межгрупповая
вариация:
- это межгрупповая
вариация:
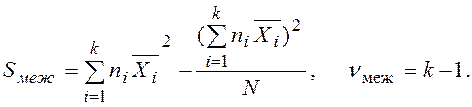
![]() - внутригрупповая
вариация:
- внутригрупповая
вариация:
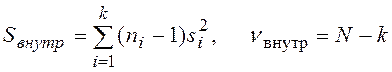 .
.
Для нахождения критических значений пользуются специальными таблицами. Если рассчитанное значение F будет больше, чем табличное для соответствующего числа степеней свободы и уровня значимости, то нулевая гипотеза о равенстве выборочных средних отвергается.
Условия применимости дисперсионного анализа:
1) каждая выборка независима от остальных выборок;
2) каждая выборка случайным образом извлечена из исследуемой совокупности;
3) совокупность нормально распределена;
4) дисперсии всех выборок не сильно отличаются друг от друга.
Пример (для двух групп с равной численностью).
Применим дисперсионный анализ для решения задачи о влиянии двух типов музыки на способность студентов решать задачи.
![]() ; s1=2,64.
; s1=2,64.
![]() ; s2=3,38.
; s2=3,38.
n1=n2=15.
Рассчитаем среднее и дисперсию выборочных средних, найдем значения межгрупповой и внутригрупповой дисперсий.
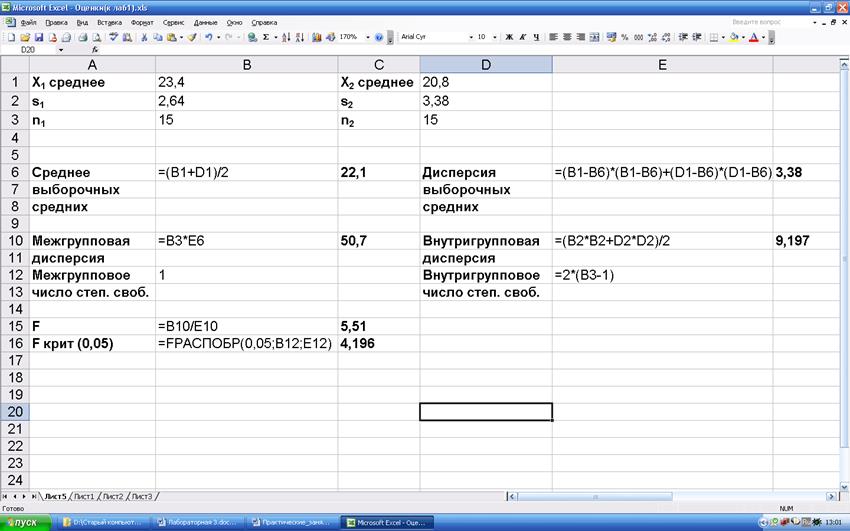
Полученное значение F больше критического. поэтому можем
заключить, что с уровнем значимости 0,05 между группами существуют
статистически значимые различия.
Задание 1. Решите с помощью дисперсионного анализа
задачу о среднем артериальном давлении при галотановой и морфиновой анестезии.
Группа с галотановой анестезией:
n1=61; ![]() ; s1=12,1;
; s1=12,1;
Группа с морфиновой анестезией:
n2=61; ![]() ;
s2=14,4.
;
s2=14,4.
Пример (для с групп с разной численностью).
Курение считают основным фактором, предрасполагающим к хроническим обструктивным заболеваниям легких. Является ли таким фактором пассивное курение? Для проверки данного предположения изучалась проходимость дыхательных путей у некурящих, активных и пассивных курильщиков. Измерялась максимальная объемная скорость середины вдоха (л/с) у некурящих, активных и пассивных курильщиков. Ее уменьшение свидетельствует о нарушении проходимости дыхательных путей. Можно ли считать этот показатель одинаковым во всех группах?
|
Группа |
Численность |
Среднее значение |
Стандартное отклонение |
|
1) Некурящие, работающие в помещении, где не курят; 2) Некурящие, работающие в накуренном помещении; 3) Курящие небольшое количество сигарет; 4) Курящие среднее количество сигарет; 5) Курящие большое количество сигарет |
202 201 197 200 200 |
3,17 2,72 2,63 2,29 2,12 |
0,74 0,71 0,73 0,7 0,72 |
Количество групп k=5, общая численность исследования N=1000 человек.
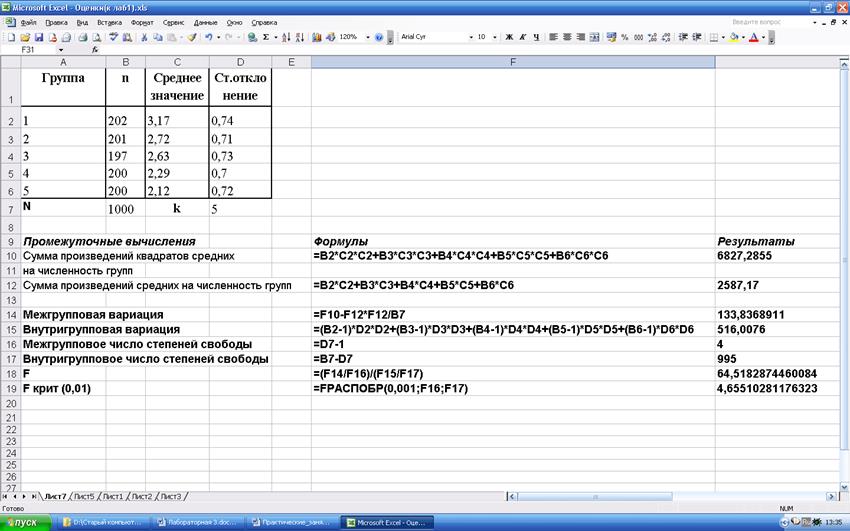
Можем опровергнуть нулевую гипотезу с уровнем значимости 0,01 и утверждать, что максимальная объемная скорость середины вдоха в группах статистически значимо различается (вероятность ошибки менее 1%).
Задание 2. 3.2. Нитропруссид натрия и дофамин – препараты, используемые при инфаркте миокарда. Эффективность этих препаратов сравнивалась в опытах на собаках. Инфаркт миокарда вызывали перевязкой коронарной артерии, после чего вводили препарат (собакам контрольной группы вводили физиологический раствор). Взвешивали пораженный участок миокарда, результат выражали в процентах от веса левого желудочка. Результаты в таблице:
|
Группа |
Число животных |
Среднее значение |
Стандартная ошибка среднего |
|
Контроль Дофамин - низкая доза - высокая доза Нитропруссид натрия |
30 13 20 20 |
15 15 9 7 |
1 2 2 1 |
Можно ли считать различия между группами статистически значимыми? (Обратите внимание, что приведено значение стандартной ошибки среднего, а не стандартного отклонения. Выполните необходимые преобразования самостоятельно, по формуле для расчета стандартной ошибки среднего).
Использование пакета Анализ данных.
Пакет Анализ данных позволяет выполнять дисперсионный анализ для исходных данных (без расчета параметров распределения).
1. В меню Сервис выберите команду Анализ данных.
Если эта команда недоступна, загрузите пакет анализа.
1. В меню Сервис выберите команду Надстройки.
2. В списке надстроек выберите Пакет анализа и нажмите кнопку OK.
3. Выполните инструкции программы установки, если это необходимо.
2. Выберите в диалоговом окне Анализ данных функцию Однофакторный
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.