Корреляционный и регрессионный анализ (Лабораторная работа № 5), страница 2

2. Коэффициент корреляции Пирсона

Нас интересует характеристика тесноты связи между двумя переменными, выраженная одним числом. Эта характеристика называется коэффициентом корреляции, обычно его обозначают r. Он может принимать значения от –1 до 1. Знак показывает направление связи (прямая – при положительном значении коэффициента или обратная – при отрицательном), а абсолютная величина – тесноту. В отсутствие связи коэффициент корреляции равен нулю. Чем ближе абсолютное значение r к единице, тем теснее связь.

Коэффициент корреляции Пирсона предназначен для описания линейной связи количественных признаков. Он требует нормального распределения.

Коэффициент корреляции Пирсона вычисляется по формуле:

.

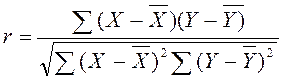Для оценки статистической значимости отличия коэффициента корреляции r можно воспользоваться критерием Стьюдента. При этом значение t вычисляется по следующей формуле:

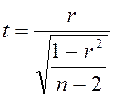;  ν = n-2.

Пример. Рассчитать коэффициенты корреляции по выборкам, для которых строили уравнения регрессии в предыдущем разделе (можно использовать функцию КОРРЕЛ).  Оценить статистическую значимость рассчитанных коэффициентов.

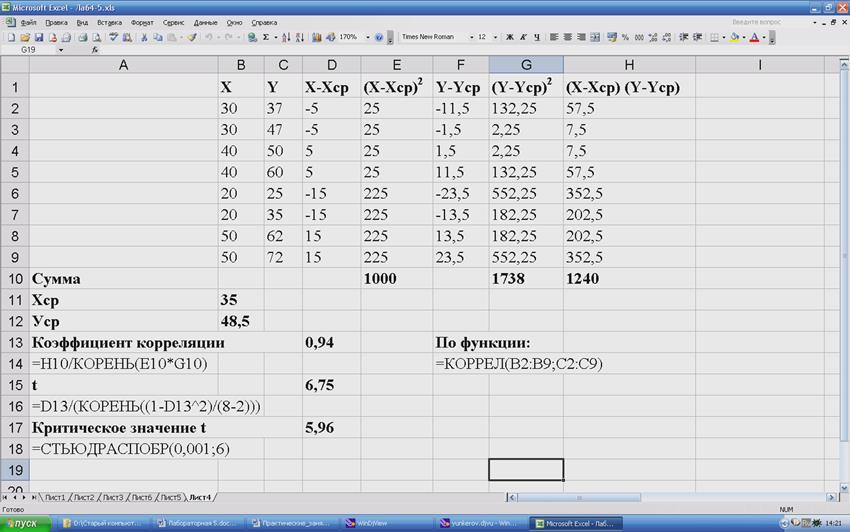
\Задание 1. Рассчитайте коэффициент корреляции для выборки из задания 1 раздела 1. Как повлияло увеличение объема выборки на тесноту корреляционной связи и статистическую значимость коэффициента корреляции?

Задание 2. Рассчитайте коэффициент корреляции между поглощенной дозой облучения и долей аберрантных клеток костного мозга (задание 4 раздела 1). Оцените статистическую значимость коэффициента корреляции.

3. Коэффициент корреляции Спирмена

Коэффициент ранговой корреляции Спирмена не требует нормальности распределения и линейной зависимости, может применяться как к количественным, так и к порядковым переменным. 

          Для вычисления коэффициента корреляции Спирмена необходимо упорядочить данные по возрастанию и заменить их реальные значения рангами. Рангом значения называется его номер в упорядоченном ряду. Если в ряду встречаются одинаковые значения, то им следует присвоить ранг, равный среднему значению занимаемых ими мест.

Коэффициент корреляции Спирмена можно рассчитать по формуле:

,

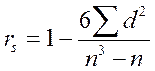где d – разность рангов каждого члена выборки.

Существуют таблицы критических значений коэффициента ранговой корреляции Спирмена для разных уровней значимости и объемов выборки (Таблица 4 Приложения). Если объем выборки больше 50, можно применить критерий Стьюдента: