Работа в MathCad: Практическое пособие

1.   ЭЛЕМЕНТЫ ТЕОРИИ МАТРИЦ

1.1.   Понятие матрицы, порядок матрицы

Определение

Прямоугольная таблица чисел называется матрицей. Матрицы обозначаются, как правило, прописными латинскими буквами (А, В, С, ...).  Матрицы состоят из элементов, в них могут быть выделены строки и столбцы. Элементы матрицы обозначают теми же буквами, что и матрицу, но только строчными, снабженными притом двумя нижними индексами. Первый из индексов соответствует номеру строки, в которой расположен соответствующий элемент, а второй - номеру столбца. Так, например, элемент а находится на пересечении второй строки и третьего столбца матрицы  А.

Количество строк и столбцов матрицы составляет понятие размерности матрицы. Говорят, что матрица А имеет размерность 3´4, если она состоит из трех строк и четырех столбцов; столбцы иногда также называют векторами.

Упражнение 1    

Указать расположение элементов матрицы  В

.

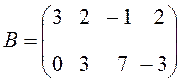Решение

1.2.   Основные типы матриц

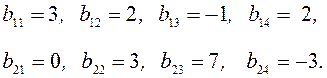
Определение

Матрица, в которой число строк равно числу столбцов, называется квадратной матрицей. Число строк (столбцов) квадратной матрицы определяет ее порядок.

Например, матрица 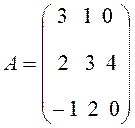  является матрицей третьего порядка.

Определение

Диагональ, идущая из северо-западного угла квадратной матрицы в юго-восточный, называется главной диагональю, другая же - второй, или второстепенной.

Различают следующие типы квадратных матриц:

а) верхняя треугольная матрица, т. е. матрица, у которой все элементы, расположенные ниже главной диагонали, равны нулю

                                                  ;

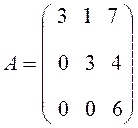б) нижняя треугольная матрица, т. е. матрица, у которой элементы, расположенные выше главной диагонали, равны нулю

                                                  ;

в) диагональная матрица, т. е. матрица, у которой все элементы, расположенные выше или ниже главной диагонали, равны нулю

                                                  ;

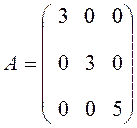г) скалярная матрица, т. е.  диагональная матрица с равными диагональными элементами

                                                  ;

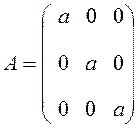д) единичная матрица, т. е. такая скалярная матрица, у которой все диагональные элементы суть единицы

                                                  .

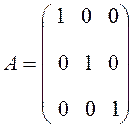Для единичной матрицы приняты следующие обозначения: I, E.

Матрица, состоящая лишь из нулевых элементов, называется нулевой матрицей и обозначается Q.

Матрица может состоять из одной строки, тогда она называется  матрицей-  строкой

.

Матрица может состоять из одного столбца, тогда она называется матрицей-столбцом, или вектором

.

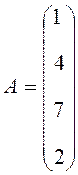В принципе можно рассматривать случай вырожденной матрицы, состоящей из одной строки и одного столбца, т. е., по существу, из одного элемента

.

1.3.   Операции над матрицами

Определение

Операция умножения матрицы на число определяется как умножение каждого элемента матрицы на это число.

Пример

Пусть задана матрица 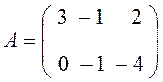, тогда матрица 3×.

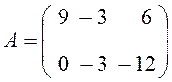Определение

Пусть даны две матрицы А и В одинаковой размерности m´n, где m - число строк в матрице, а  n - число столбцов. Тогда матрица С размерности m´n называется суммой матриц А и В, если каждый элемент матрицы С является суммой соответствующих элементов матриц  А и В

 , i = 1, 2, ..., m; j = 1, 2, ..., n.

Пример

,  .

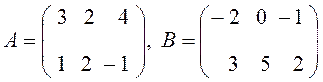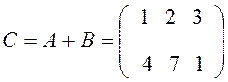Замечание

Как видно из определения, складывать можно матрицы только одинаковой структуры. В частности, для матриц  и 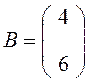 операция сложения не определена.

Упражнение 2

Даны две матрицы 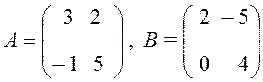.  Найти матрицу  С = 3А – 2В.

Решение

.

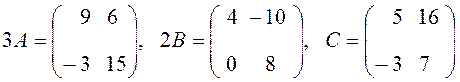Отметим очевидные свойства операций сложения матриц и умножения матрицы на число:

1.   А + В = В + А;

2.   А + Q= А;

3.   А + (-А) =Q;

4.   А + (В + С) = (А + В) + С;

5.   (l + m) А = lА + mА,  l, m Î R;

6.   lА + lВ = l (А + В);

7.   1×А = А;

8.   l(mА) = (lm)А.

Определение

Пусть даны две матрицы,  A (m´n) и  В (n´p)

                    А = 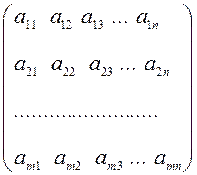,         B =  ,

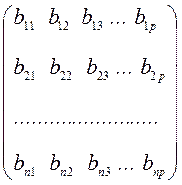причем число столбцов матрицы А равно числу строк матрицы В.

Произведением матрицы А на матрицу В называется матрица

С = ,

элементы которой вычисляются по формулам

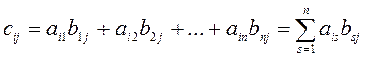  ( i = 1, 2, .,m; j = 1, 2, .., p ).

Согласно этому определению, не всякие две матрицы можно перемножить. Произведение двух матриц определено тогда и только тогда, когда число столбцов матрицы, стоящей слева в этом произведении, равно числу строк матрицы, стоящей справа. Что же касается формулы, по которой вычисляются элементы результирующей матрицы, то ее можно интерпретировать как сумму попарных произведений элементов строки матрицы, стоящей слева, на элементы столбца матрицы, стоящей справа. Иначе говоря, для получения элемента результирующей матрицы  следует умножить i-ю строку  матрицы, стоящей слева, на  j-й столбец матрицы, стоящей справа.

Упражнение 3

Пусть даны матрицы

,  .

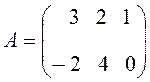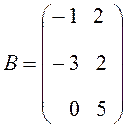Составить произведения матриц  C = AB,  D = BA.

Решение  

1. Найдем элементы матрицы  С = АВ.

C = ,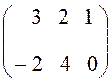

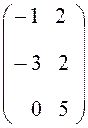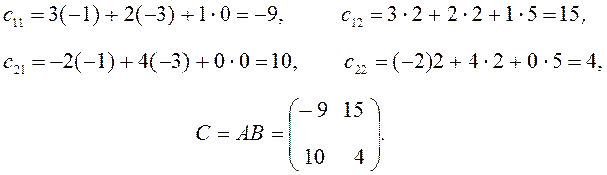
2. Найдем элементы матрицы  D = BA .

D = ,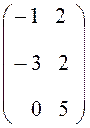

.

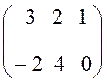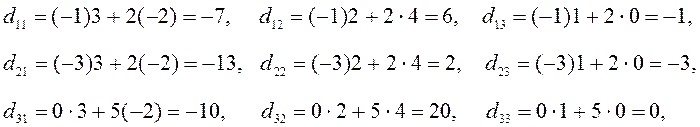
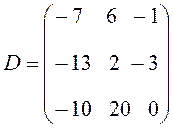Сравнивая матрицы С  и  D, нетрудно заметить, что они не только состоят из разных элементов, но и имеют разную размерность. Таким образом, отсюда следует, что произведение матриц, вообще говоря, не подчиняется перестановочному закону, т. е.  АВ ¹ ВА.