Определение
Минор D![]() элемента а
элемента а![]() ,
полученный в результате вычеркивания i-й строки и j-го столбца
исходного определителя, умноженный на (–1)
,
полученный в результате вычеркивания i-й строки и j-го столбца
исходного определителя, умноженный на (–1)![]() ,
называется алгебраическим дополнением этого элемента и обозначается А
,
называется алгебраическим дополнением этого элемента и обозначается А![]() .
.
Отметим, что если сумма индексов ( i + j ) – четное
число, то А![]() = D
= D![]() , если же нечетное, то А
, если же нечетное, то А![]() = – D
= – D![]() .
.
Пример
Даны миноры: D![]() = 6, D
= 6, D![]() = 5, D
= 5, D![]() = 1, D
= 1, D![]() = 3. Их алгебраическими дополнениями
будут: А
= 3. Их алгебраическими дополнениями
будут: А![]() =
6, А
=
6, А![]() =
–5, А
=
–5, А![]() =
–1, А
=
–1, А![]() =
3.
=
3.
Теорема (свойство 5)
Определитель матрицы А равен сумме произведений всех элементов строки или столбца на их алгебраические дополнения.
Доказательство теоремы можно найти в [1].
Пример
Найдем величину определителя 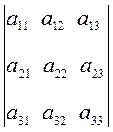 ,
используя свойство 5. Для этого разложим определитель по элементам второго
столбца:
,
используя свойство 5. Для этого разложим определитель по элементам второго
столбца:
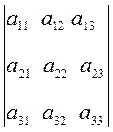 = а
= а![]() А
А![]() + а
+ а![]() А
А![]() + а
+ а![]() А
А![]() = – а
= – а![]() D
D ![]() + а
+ а![]() D
D![]() – а
– а![]() D
D![]() .
.
.
Упражнение 7. Найти определитель 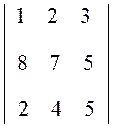 .
.
Решение
Разложим определитель по элементам первой строки
D = 1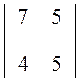 – 2
– 2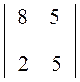 + 3
+ 3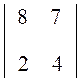 = 7 – 60 + 54 = 1.
= 7 – 60 + 54 = 1.
Отметим, что использование свойства 5 в принципе позволяет вычислять определители любых порядков.
Упражнение 8. Найти определитель 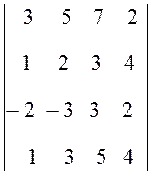 .
.
Решение
D = 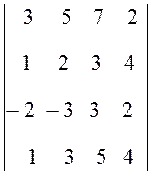 =
= 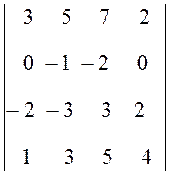 = 2
= 2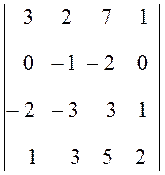 =
=
а![]() - а
- а![]()
= 2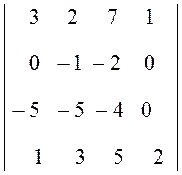 =
2
=
2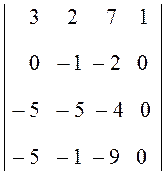 =
2(–1
=
2(–1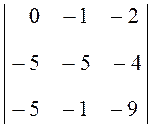 +
+
a3 – a1 a4 – 2a1
+ 0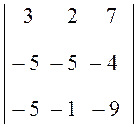 + 0
+ 0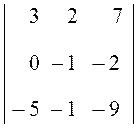 + 0
+ 0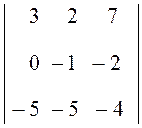 ) = –2
) = –2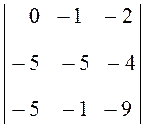 =
=
= –2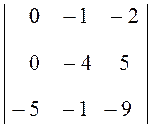 =
–2(–5)
=
–2(–5)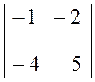 =
10( –5 – 8) = –130.
=
10( –5 – 8) = –130.
a2 – a3
В процессе решения указаны преобразования определителя: так,
например, преобразование а![]() - а
- а![]() означает,
что из всех элементов строки а
означает,
что из всех элементов строки а![]() вычтены
все элементы строки а
вычтены
все элементы строки а![]() .
.
Определение
Линейной комбинацией строк (столбцов) называется выражение (α 1 b1+ + α 2 b2 + … + α n bn), где α 1 , α 2 , …, α n Î R ; a1, a2 , …, an (b1, b2 … bn) - строки (столбцы) матрицы А.
Следствия
1. Определитель, в котором строка или столбец состоят из нулевых элементов, равен нулю.
2. Определитель, в котором две строки или два столбца состоят из одинаковых элементов, равен нулю.
3. Определитель, в котором строка (столбец) является линейной комбинацией других строк (столбцов), равен нулю.
Первое следствие является очевидным, для этого достаточно разложить определитель по строке (столбцу), состоящей из нулевых элементов.
Второе и третье следствия опираются на свойство 4 и их доказательство представляется очевидным.
Вычислить значения определителей четвертого порядка.
1. 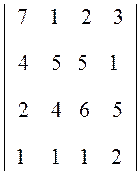 . Ответ:
121.
. Ответ:
121.
2. 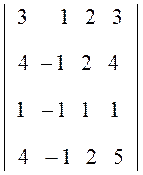 . Ответ:
-5.
. Ответ:
-5.
3. 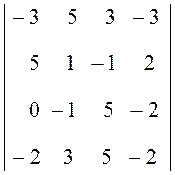 . Ответ:
-188.
. Ответ:
-188.
4. 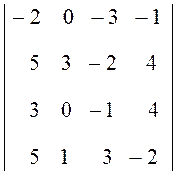 . Ответ:
-185.
. Ответ:
-185.
MathCAD относится к языкам интерпретаторам, таким как MatLab, Mathematica, Lisp и т.д., в отличие от языков компиляторов, к которым относится Pascal, C++, Basic, Fortran и т.д.
Для запуска программы, написанной на языке MathCAD и сохраненной в фале с расширением .MCD, необходимо использовать среду MathCAD.
MathCAD является средой для работы с формулами, числами, текстами и графикой.
MathCAD позволяет записывать на экране компьютера формулы в их привычном виде. Например, так выглядит формула для расчета корня квадратного уравнения, в программном модуле на языке Basic (Рис. 3.1)
Рис. 3.1. Вид формулы на языке Basic
В MathCAD эта же формула выглядит так (Рис. 3.2)

Рис. 3.2. Вид формулы в MathCAD
Объединяя на одном листе пояснительный текст, математические выкладки и результаты расчета в виде текстовой и графической информации MathCAD позволяет получить законченный правильно оформленный документ.
Знак равенства в MathCAD используется в различных формах написания и значения. Ниже рассмотрены некоторые варианты.
1. Присвоение значений переменным или функциям.
Синтаксис.
|
имя переменной или функции |
знак ":=" |
присваиваемое значение |
|
Пример, alfa:=56.25 |
||
Варианты ввода знака ":="
· нажать одновременно клавиши "Shift" и ":";
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.