3.Ввести сопроводительный текст "Вариант №1".
4. Вычислить определитель матрицы А, используя функцию MathCAD - |А| и сохранить результат в переменной - b,
3.Ввести сопроводительный текст "Вариант №2".
4. Вычислить определитель матрицы А, используя элементы матрицы А
= 
.
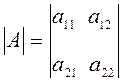и сохранить результат расчета в переменной – b1,
6. Посмотреть содержание переменных А, b, b1.
Листинг программы (Пример 5.11) приведен на (Рис. 5.11).
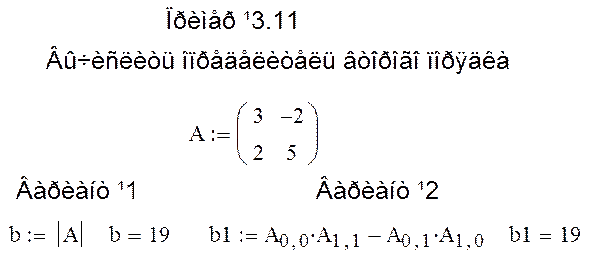
Рис. 5.11. Листинг программы (Пример 5.11)
Пример 5.12. Вычислить определитель третьего порядка
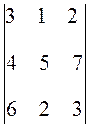
1.Ввести сопроводительный текст "Пример №3.12 Вычислить определитель третьего порядка".
2. Ввести переменную – A, присвоить переменной матрицу-шаблон размером 3х3, заполнить элементы матрицы-шаблона цифрами.
3.Ввести сопроводительный текст "Вариант №1".
4. Вычислить определитель матрицы А, используя функцию MathCAD - |А| и сохранить результат в переменной - D,
3.Ввести сопроводительный текст "Вариант №2".
4. Вычислить определитель матрицы А, используя элементы матрицы А
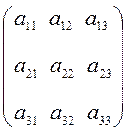
D1 = 
+
+
–(
+
+
).
и сохранить результат расчета в переменной – D1,
При вводе расчетного соотношения по варианту №2 формула оказывается очень протяженной и выходит за рамки листа. Перенос части формулы на вторую строку в MathCAD возможен только перед введением оператора "+". Для перехода на вторую строку при наборе выражения необходимо перед вводом оператора "+" нажать клавиши "Ctrl" + "Enter". В этом случае на первой строке автоматически вставляются знаки многоточия, а на второй строке знак "+", как показано на Рис. 5.11.
6. Посмотреть содержание переменных А, D, D1.
Листинг программы (Пример 5.12) приведен на (Рис. 5.11).
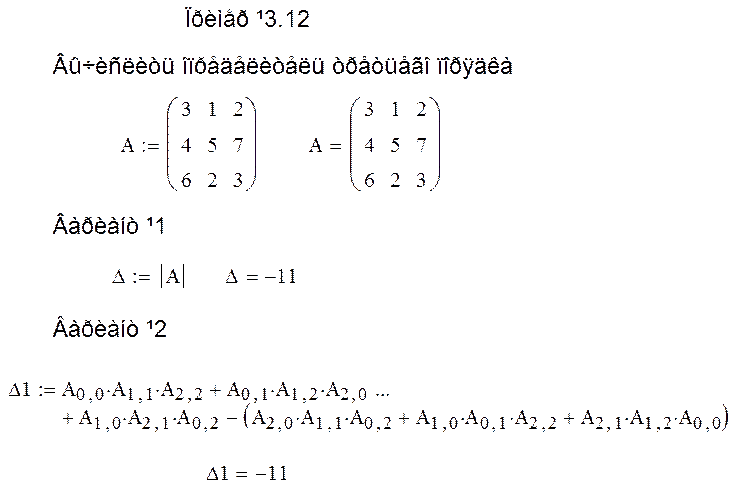
Рис. 5.11. Листинг программы (Пример 5.12)
Пример 5.13. Вычислить определитель третьего порядка по методу Саррюса
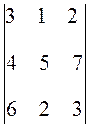
1.Ввести сопроводительный текст "Пример №3.13 Вычислить определитель третьего порядка по методу Саррюса
2. Ввести переменную – A, присвоить переменной матрицу-шаблон размером 3х3, заполнить элементы матрицы-шаблона цифрами.
3.Ввести сопроводительный текст "Вариант №1".
4. Вычислить определитель матрицы B, используя функцию MathCAD - |B| и сохранить результат в переменной - D,
3.Ввести сопроводительный текст "Вариант №2".
4. Преобразовать матрицу В к виду по правилу Саррюса и сохранить результат в переменной АВ. Вычислить определитель матрицы АB, используя метод Саррюса. По правилу Саррюса определитель дополняется двумя первыми столбцами:
.
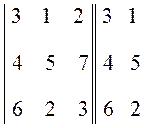В полученной структуре проводятся три левых и три правых диагонали:
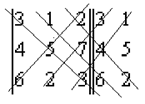
Произведение чисел, расположенных на главной и параллельных ей диагоналях, берется со знаком ²+², в то время как произведение чисел, расположенных на второй и параллельных ей диагоналях, берется со знаком ²-².
Сохранить результат расчета в переменной – D1,
При вводе расчетного соотношения по варианту №2 формула оказывается очень протяженной и выходит за рамки листа. Перенос части формулы на вторую строку в MathCAD возможен только перед введением оператора "+". Для перехода на вторую строку при наборе выражения необходимо перед вводом оператора "+" нажать клавиши "Ctrl" + "Enter". В этом случае на первой строке автоматически вставляются знаки многоточия, а на второй строке знак "+", как показано на Рис. 5.11.
6. Посмотреть содержание переменных А, D, D1.
Листинг программы (Пример 5.13) приведен на (Рис. 3.1).
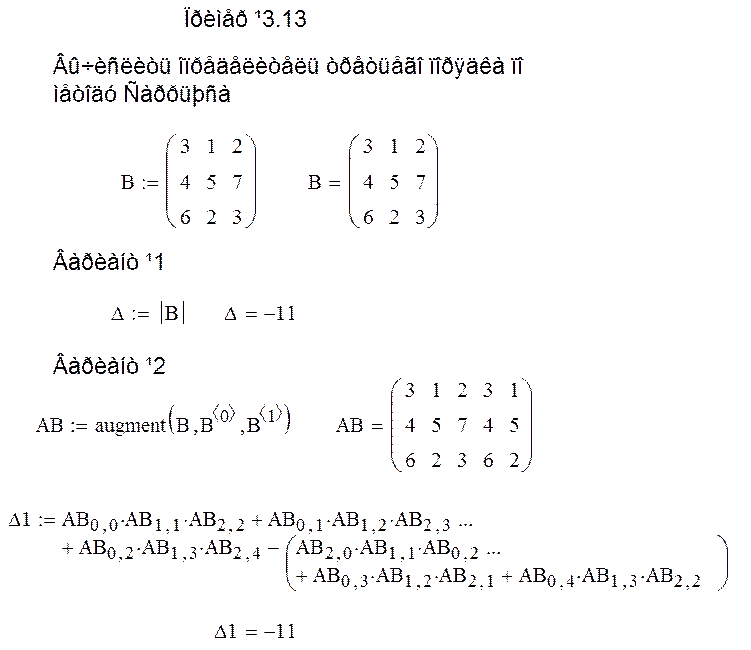
Рис. 5.13. Листинг программы (Пример 5.13)
Пример 5.14. Транспонировать и вычислить обратную матрицу из матрицу
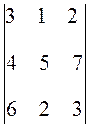
1.Ввести сопроводительный текст "Пример №3.14. Транспонировать и вычислить обратную матрицу".
2. Ввести переменную – A, присвоить переменной матрицу-шаблон размером 2х3, заполнить элементы матрицы-шаблона цифрами.
3. Произвести транспонирование матрицы А, используя функцию MathCAD - 
и
сохранить результат в переменной - AT,
4. Вычислить матрицу обратную А, используя функцию MathCAD - 
и
сохранить результат в переменной - AO,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.